A energia potencial de uma partícula de massa numa dada posição é descrita pela função (em Joules, sendo em metros), mostrada na figura abaixo.
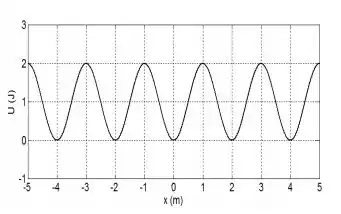
- Calculo a força que atua na partícula para todo .
- Calcule a frequência angular de pequenas oscilações em torno de .
- A posição em função do tempo.
- A velocidade em função do tempo da partícula, .
- O módulo da velocidade da partícula quando esta se encontra na posição .
Considerando que a partícula é colocada em repouso na posição no instante de tempo e realiza pequenas oscilações em torno de , determine:
Sugestão: utilize a série de Taylor de em torno de .
Passo 1
a):
Bom, vamos lembrar daquela equação de física 1:
Sendo:
Então:
Passo 2
b):
Aqui a gente vai usar a sugestão da série de Taylor.
A série de Taylor pra , em torno de é:
Então, reescrevendo
Com:
Show! Mas olha só:
Isso ai se parece com:
Então:
E como:
Passo 3
c) O que o enunciado nos diz é:
A velocidade inicial é essa porque ele diz que a partícula sai do repouso.
Bom, a função segue o padrão:
Então a gente só precisa descobrir a fase , já que já sabemos
Assim:
Como:
E como:
Por que zero e não Porque a gente viu que o cosseno tem que ser maior que zero.
Então:
Ai:
Passo 4
d):
Ai é so derivar
Passo 5
e):
Ai é só a gente tentar maximizar a função:
Isso acontece quando . Por que? Porque ai vamos ter o maior valor positivo que a função pode alcançar:
Resposta
a):
b):
c):
d):
e):