PSUB de Física 2 da USP - 2018

O gráfico representa uma posição de uma massa ligada a mola. No instante indicado pela linha tracejada, qual afirmação é correta?

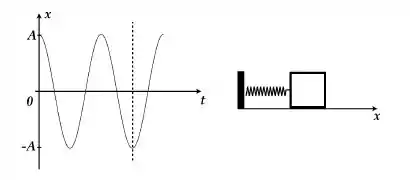
1. a velocidade é nula e força restauradora para direita.
2. a velocidade é negativa e força restauradora para esquerda.
3. a velocidade é negativa e força restauradora para direita.
4. a velocidade é positiva e força restauradora para direita.
5. a velocidade é nula e força restauradora para esquerda.

Duas esferas uniformes estao picotadas sobre um eixo horizontal que passa pelo ponto O. Dado que o momento de inércia da esfera passando pelo seu centro podemos afirmar que a esfera com maior período de oscilação é aquela com:

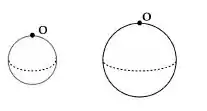
a) a maior massa.

b) o menor momento de inércia rotacional

c) a menor massa.

d) o maior raio.

e) o maior momento de inércia rotacional.

Um oscilador harmônico amortecido é formado por uma massa , uma mola de constatne elástica , e uma amortecedor com constante de . Ao aplicar uma força externa e , a amplitude do movimento será

1. nenhuma das demais alternativas
2. 10 mm
3. 50 mm
4. 100 mm
5. 1 m

Um oscilador harmônico amortecido unidimensional é formado por uma massa , uma mola de constante elástica , e um amortecedor com constante de amortecimento . No instante a massa está localizada em e possui velocidade . Qual gráfico melhor representa a massa em função do tempo?

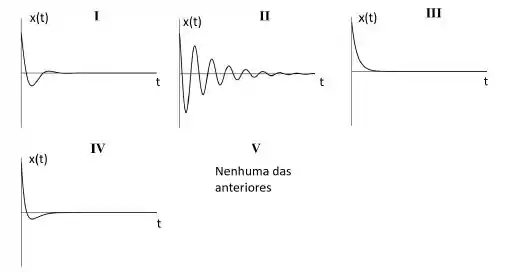
1. V
2. III
3. IV
4. II
5. I

A função que representa o resultado da interferência de duas ondas transversais, cujas funções de onda são

Uma haste rígida homogênea de comprimento Le massa M está suspensa, podendo girar sem atrito em torno do ponto O, onde há um pino de suspensão. A extremidade superior da barra está ligada a duas molas dispostas horizontalmente em lados opostos da barra, com constante k, estando ambas relaxas quando a barra está na posição vertical. No instante t=0, a barra é deslocada para a esquerda até um ângulo e liberada com velocidade angular inicial nula. Assuma q as molas permanecem sempre na horizontal.

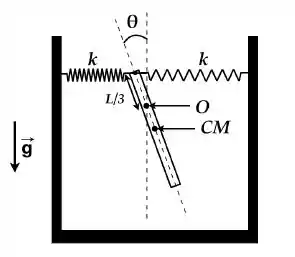
a) Esboce o diagrama de forças que agem sobre a barra no instante em que a barra faz um ângulo com a vertical.

b) Adote um sistema de coordenadas com uma base de versores e escreva as forças identificadas no ítem a nessa base de versores.

c) Obtenha a equação diferencial que descreve o movimento da barra.

d) Determine o período de oscilação da barra.

e) Obtenha a função que descreve o movimento de oscilação da barra.