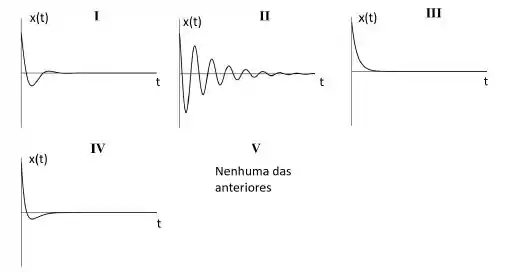
Um oscilador harmônico amortecido unidimensional é formado por uma massa , uma mola de constante elástica , e um amortecedor com constante de amortecimento . No instante a massa está localizada em e possui velocidade . Qual gráfico melhor representa a massa em função do tempo?
- V
- III
- IV
- II
- I
Passo 1
O regime de amortecimento aqui é o crítico, já que . A solução geral para a posição do oscilador é
Logo
Passo 2
Aplicando as condições iniciais
Logo
e
o que mostra que o gráfico que melhor representa a posição é o IV, já que o oscilador parte da posição x(0)=0,1 em t=0 se movendo na direção de x decrescente , passando pela origem em t=1/5 e atinge o repouso em t=2/5s, quando inverte seu movimento.
Resposta
Letra c
Exercícios de Livros Relacionados
137. Uma máquina de 200k g se apoia sobre quatro suportes no chão, cada um dos quais possui uma constante de mola efetiva k = 250k N / m e um coeficiente de amortecimento viscoso efetivo c = 1000 N ⋅
138. Represente graficamente a resposta x do corpo de 20k g ao longo do intervalo de tempo 0 ≤ t ≤ 1 segundo. Determine os valores máximo e mínimo de x e seus respectivos instantes de tempo. As condiç
Para uma criança em um balanço, a amplitude cai em um fator de 1 e em cerca de oito períodos, se nenhuma energia mecânica adicional for fornecida ao sistema. Estime o fator Q para este sistema.
Para o cilindro do Prob. 8/8, determine o deslocamento vertical x, medido para baixo no sentido positivo em milímetros, a partir da posição de equilibro, em termos do tempo t, em segundos, medido a pa
Em um oscilador amortecido com m = 250 g , k = 85 N / m e b = 70 g / s , qual é a razão entre a amplitude das oscilações amortecidas e a amplitude inicial após 20 ciclos?