Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Pêndulo de Torção

Ver Teoria
Exercício 1012345678911

Enunciado

Uma haste rígida homogênea de comprimento Le massa M está suspensa, podendo girar sem atrito em torno do ponto O, onde há um pino de suspensão. A extremidade superior da barra está ligada a duas molas dispostas horizontalmente em lados opostos da barra, com constante k, estando ambas relaxas quando a barra está na posição vertical. No instante t=0, a barra é deslocada para a esquerda até um ângulo π 30 r a d e liberada com velocidade angular inicial nula. Assuma q as molas permanecem sempre na horizontal.

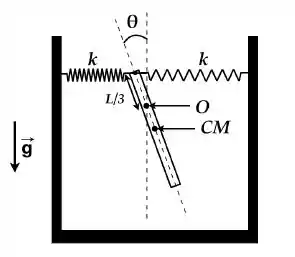
a) Esboce o diagrama de forças que agem sobre a barra no instante em que a barra faz um ângulo θ com a vertical.

b) Adote um sistema de coordenadas com uma base de versores e escreva as forças identificadas no ítem a nessa base de versores.

c) Obtenha a equação diferencial que descreve o movimento da barra.

d) Determine o período de oscilação da barra.

e) Obtenha a função θ t que descreve o movimento de oscilação da barra.

Passo 1

a)

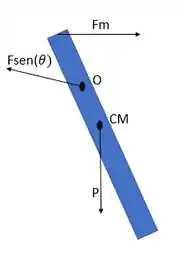
Passo 2

b) temos que

F m = 2 k x = - 2 k - 1 3 s e n θ = 2 k L 3 s e n θ

O somatório das forças é

∑ τ = I o x = I d θ 2 d t 2

portanto

I o = I C M + M L 2 = M L 2 12 + M L 6 2 = M L 2 9

Passo 3

c)

∑ τ = τ p + τ F M

Temos que

τ F M = - 2 k L 2 s i n θ c o s θ 9

τ P = - L 6 M g s i n θ h

Somando, chegamos a

∑ τ = M L 2 9 d 2 θ d t 2

Como θ ≪ 1     temos s e n θ = θ e c o s θ = 1 .

Logo

d 2 θ d t 2 = - 3 2 g L + 2 k M θ  

Passo 4

d)

ω 2 = 3 2 g L + 2 k M

Com T = 2 π ω

T = 2 π 3 2 g L + 2 k M

Passo 5

e) As condições iniciais são

θ 0 = π 30

d θ d t = 0  

Onde θ t = θ M cos ⁡ ω t + ϕ

d θ d t 0 = - ω θ sin ⁡ ϕ = 0

Logo

ϕ = 0   o u   π

Portanto a solução será

θ t = π 30 c o s ⁡ ( ω t ) , com ω = 3 2 g L + 2 k M

Resposta

Ei, a resposta está no passo a passo :)

Exercícios de Livros Relacionados

O balanço de um relógio antigo oscila com uma amplitude angular de πrad e um período de 0,500 s . Determine (a) a velocidade angular máxima do balanço, (b) a velocidade angular no instante em que o de
35. Um relógio da quatro tiques a cada segundo; cada tique corresponde à metade do período. A roda catarina do relógio consiste em uma fina camada circular com raio de 0,55c m conectada ao conjunto da
52.Um macaco mecânico de 1,80k g é suspenso por um pivô localizado a uma distância de 0,250m de seu centro de massa e começa a oscilar como um pêndulo físico. O período da oscilação com ângulo pequeno
13.6E Considere o pêndulo de torção mostrado na Figura 13.5 do texto. O disco tem massa de 200g e raio de 10,0cm . A constante de torção da barra vale 3,00 × 10 - 2Nm . Qual é o período de oscilação d
13.7E Reconsiderando o pêndulo do Exercício 13.6. A) qual é sua energia mecânica se no instante em que o ângulo de torção é θ = 5,00 ° sua velocidade angular é 0,600rad/s ?