Duas esferas uniformes estao picotadas sobre um eixo horizontal que passa pelo ponto O. Dado que o momento de inércia da esfera passando pelo seu centro podemos afirmar que a esfera com maior período de oscilação é aquela com:
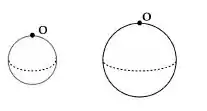
a) a maior massa.
b) o menor momento de inércia rotacional
c) a menor massa.
d) o maior raio.
e) o maior momento de inércia rotacional.
Passo 1
Quando a linha que une o ponto O com CM de cada esfera gira de um ângulo com repeito a vertical, o torque exercido pelo peso é
O momento de inércia das esferas para a rotação em torno do eixo que passa por O e , portanto, paralelo àquele que passa pelo centro de massa e a uma distância de R desse última é
De forma que da segunda lei de Newton para rotação , temos
E portanto, o período natural de oscilação dessas esferas em torno de O é
O maior raio deve então produzir o maior período de oscilação.
Resposta
Letra d