Exercícios Mais Acessados UTFPR - Young Freedman Vol 2 - 12°ed de Física 2 da UTFPR - Movimento Periódico

(Cap 13 - Ex 27) Você observa um objeto movendo-se em . Quando o objeto é deslocado até a direita da sua posição de equilíbrio, sua velocidade é igual a para a direita, e sua aceleração é igual a para a esquerda. A que distância máxima desse ponto irá o objeto se mover antes de parar momentaneamente e depois recomeçar a se mover para a esquerda?

(Cap 13 - Ex 1) A corda de um piano emite um lá médio vibrando com uma frequência primaria igual a 220 Hz. a) Calcule o período e a frequência angular. b) Calcule a frequência angular de uma soprano emitindo um lá uma oitava acima que é igual a duas vezes a frequência da corda do piano.

(Cap 13 - Ex 45) Uma maçã pesa . Quando você a suspende na extremidade de uma mola longa de massa desprezível e constante igual a , ela oscila para cima e para baixo com um . Quando você interrompe a oscilação e deixa a maçã oscilar lateralmente em um ângulo pequeno, a frequência do pêndulo simples é igual à metade da frequência da oscilação vertical. (Como o ângulo é pequeno, a oscilação lateral não produz variação no tamanho da mola.) Determine o comprimento da mola quando ela não está esticada (sem a maçã).

(Cap 13 - Ex 60) Uma força propulsora variando senoidalmente é aplicada a um oscilador harmônico amortecido de massa e constante da mola . Se a constante de amortecimento possui valor , a amplitude é quando a frequência angular da força propulsora é igual a . Em termos de , qual é a amplitude para a mesma frequência angular da força propulsora e a mesma amplitude da força propulsora quando a constante de amortecimento for: ? ?

(Cap 13 - Ex 18) Uma massa de oscilador em uma mola tem a velocidade em função do tempo dada por . Qual é o período; a amplitude; a aceleração máxima da massa; a constante da mola?

(Cap 13 - Ex 2) Se um objeto sobre uma superfície horizontal, sem atrito, é preso a uma mola, deslocado e depois libertado, ele irá oscilar. Se ele for deslocado 0,120 m da sua posição de equilíbrio e libertado com velocidade inicial igual a zero, depois de 0,800 s verifica-se que o seu deslocamento é de 0,120 m no lado oposto e que ele ultrapassou uma vez a posição de equilíbrio durante esse intervalo. Ache (a) a amplitude, (b) o período, (c) a frequência.

(Cap 13 - Ex 57) Uma força de amortecimento atua sobre um rato infeliz de que se move preso a extremidade de uma mola cuja constante é . Se a constante tem um valor igual a , qual é a frequência de oscilação do rato? Para qual valor da constante o movimento é criticamente amortecido?

(Cap 13 - Ex 32) Um gato com massa igual a está preso por arreios a uma mola ideal de massa desprezível e oscila verticalmente em . A amplitude do movimento é . No ponto mais alto do movimento, a mola está na posição natural, ou seja, não está esticada. Calcule a energia potencial elástica da mola (considerando-a igual a zero quando não ela não está esticada) a energia cinética do gato, a energia potencial gravitacional do sistema em relação ao ponto mais baixo do movimento e a soma dessas três energias quando o gato está no ponto mais alto do movimento; no ponto mais baixo; no ponto de equilíbrio.

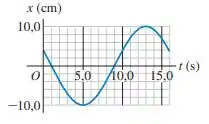
(Cap 13 - Ex 4) O deslocamento de um objeto oscilando em função do tempo é mostrado na Figura 13.30. Quais são (a) a frequência; (b) a amplitude; (c) o período; (d) a frequência angular desse movimento?

(Cap 13 - Ex 8) Quando uma massa de 0,750 kg oscila em uma mola ideal, a frequência é igual a 1,33 Hz. Qual será a frequência se 0,220 kg forem adicionados à massa original, e (b) subtraídos à massa original? Tente resolver este problema sem achar a constante da mola.

(Cap 13 - Ex 45) Uma massa de oscila em uma mola de constante igual a com um período de . Esse sistema é amortecido ou não? Como você sabe disso? Se for amortecido, encontre a constante de amortecimento . Esse sistema é não amortecido, subamortecido, criticamente amortecido ou superamortecido? Como você sabe que é assim?

(Cap 13 - Ex 31) Um corpo de sobre um trilho de ar horizontal, sem atrito, é preso a uma mola fixa ideal de constante . No instante que você efetua medições sobre o corpo, ele estará se movendo a e está a de seu ponto de equilíbrio. Use a conservação de energia para calcular a amplitude do movimento e a velocidade máxima do corpo. qual é a frequência angular das oscilações?

(Cap 13 - Ex 13) A ponta da agulha de uma máquina de costura se move com MHS ao longo de um eixo com uma frequência igual a . Em os componentes da posição e da velocidade são respectivamente, e . Ache o componente da aceleração da agulha para . Escreva equações para os componentes da posição, da velocidade e da aceleração do ponto considerado em função do tempo.

(Cap 13- Ex 72) Um bloco de massa igual a está submetido a uma força restauradora elástica e a constante da força é igual a . Faça um gráfico da energia potencial em função do deslocamento no intervalo de até . Em seu gráfico, adote a escala no eixo vertical e no eixo horizontal. O bloco inicia o movimento oscilatório com uma energia potencial igual a e uma energia cinética igual a . Examinando o gráfico, responda às perguntas seguintes. Qual é a amplitude da oscilação? Qual é a energia potencial quando o deslocamento é igual a metade da amplitude? Para qual deslocamento a energia potencial é igual a igual a energia cinética? Qual é o valor do ângulo de fase , sabendo que a velocidade inicial é positiva e o deslocamento inicial é negativo?