Física Termodinâmica e Ondas – Young e Freedman – 12 edição – Capítulo 13 – Exercício 1.
(Cap 13 - Ex 1) A corda de um piano emite um lá médio vibrando com uma frequência primaria igual a 220 Hz. a) Calcule o período e a frequência angular. b) Calcule a frequência angular de uma soprano emitindo um lá uma oitava acima que é igual a duas vezes a frequência da corda do piano.
Passo 1
Falai meus amores, tudo bem?
Bora resolver mais uma comigo?
Encostaa
Legal, o enunciado nos fornece uma frequência primaria de , para resolver o item (a), nos podemos usar a formula, onde o período é o inverso da frequência
Ou seja, substituindo na fórmula, iremos obter
Passo 2
Para realizarmos o calculo da frequência angular , iremos utilizar a teoria, onde ela nos diz que, a frequência angular, e vezes a frequência , portanto, a definição de é
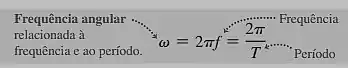
Sabemos que representa uma taxa de variação de uma grandeza angular, que não necessariamente esta relacionada ao movimento de rotação, pois ela é sempre medida em radianos.
Sua formulação dar – se por :
Então, como temos a frequência, que nos foi fornecida pelo enunciado, basta substituir, logo:
Passo 3
Agora vamos para o item (b). Como a frequência é duas vezes maior que a frequência anterior, então, reformulando os valores, temos
Temos que o período é o inverso da frequência
Ou seja, substituindo na fórmula, iremos obter
Efetuando o calculo da frequência angular partindo dos novos dados, teremos:
Então