Exercícios Mais Acessados UTFPR - Young Freedman Vol 2 - 12°ed de Física 2 da UTFPR - Ondas

(Cap 15- Ex 8) Uma onda se desloca na água em linha reta sobre um lago é descrita pela equação

Onde y é o deslocamento perpendicular à superfície sem perturbações do lado. a) Quanto tempo leva para que uma configuração completa de onda passe por uma pescador em um barco ancorado, e que distancia horizontal a crista da onda percorre nesse tempo? b) Qual é o numero da onda e o numero de ondas por segundo que passam pelo pescador? c) Com que velocidade uma crista de onda se desloca ao passar pelo pescador?, e qual a velocidade máxima de seu flutuador de cortiça quando a onda o faz oscilar para cima e para baixo?

(Capítulo 15.Exercícios – Exercícios 29) Suponha que o pulso que se desloca para a esquerda no Exercicio 15.28 esteja abaixo do nivel da corda não esticada, em vez de acima. Desenhe os mesmo diagramas que voce desenhou naquele exercicio.

(Cap 15- Ex 6) Uma certa onda transversal é descrita por

Determine para esta onda a) a amplitude; b) o comprimento de onda; c) a frequência; d) a velocidade de propagação; e) a direção de propagação.

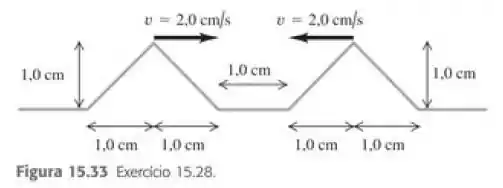
(Capítulo 15.Exercícios – Exercícios 28) Dois pulsos ondulatórios triangulares estão se aproximando em uma corda esticada, como indicado na Figura 15.33. Os dois pulsos são idênticos e se deslocam com velocidade igual a 2,0 cm/s. A distancia entre as extremidades dianteira dos pulsos é igual a 1,0 cm para . Desenhe a forma da corda para

(Capítulo 15.Exercícios – Exercício 21) Um avião a jato em decolagem pode produzir um som de intensidade a de distância. Você, contudo, prefere o som tranquilo de uma conversa normal, que é . Suponha que o avião se comporte como uma fonte sonora pontual. a) Qual é a mínima distância do aeroporto que a sua casa precisa ter para que você possa conservar a sua paz de espírito? b) Qual é a intensidade sonora que chega a sua amiga se ela mora duas vezes mais longe da pista do que você? c) Que potência sonora o jato produz ao decolar?

(Cap 15- Ex 1) A velocidade do som no ar a é igual a . a) Qual é o comprimento de onda da onda sonora com frequência igual a , correspondente à nota de um piano, e quantos milis-segundos leva cada vibração? b) Qual é o comprimento de onda de um som uma oitava mais alto do que a nota do item (a)?

(Cap 15 - Ex 9) Quais das seguintes funções satisfazem a função de onda dada pela Equação (15.2)? a) ; b) ; c) ; d) Para a onda do item (b), escreva a equação para a velocidade transversal e a aceleração transversal de uma partícula no ponto x.

(Capítulo 15.Exercícios – Exercícios 23) Fornecimento de energia. Por meio de medições, você determina que ondas sonoras estão se propagando igualmente em todas as direções a partir de uma fonte pontual e que a intensidade é igual a a uma distância de da fonte. a) Qual é a intensidade a uma distância de da fonte? b) Quanta energia sonora a fonte emite em uma hora se a potência fornecida for constante?

(Capítulo 15.Exercícios – Exercício 15) Uma das extremidades de um fio é presa a um dos ramos de um diapasão eletricamente excitado com uma frequência igual a . A outra extremidade passa sobre uma polia e suporta um objeto com massa igual a . A densidade linear do fio é igual a . a) Qual é a velocidade de propagação de uma onda transversal na corda? b) Qual é o comprimento de onda? c) Como suas respostas dos itens (a) e (b) se modificam se a massa do objeto aumentar para ?

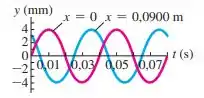
(Cap 15 - Ex 11) Uma onda senoidal propaga-se ao longo de uma corda esticada sobre o eixo . O deslocamento da corda em função do tempo é indicado na figura 15.30 para partículas nos pontos e .

1. Qual é a amplitude da onda?
2. Qual é o período da onda?
3. Informamos a você que a distância entre os pontos e é menor do que o comprimento de onda. Determine a velocidade e o comprimento de onda quando ela se propaga no sentido .
4. Supondo agora que a onda se propague no sentido , determine a velocidade e o comprimento de onda.
5. Seria possível determinar de forma não ambígua o comprimento de onda calculado dos itens e se você não usasse o dado de a distância entre os pontos ser menor do que o comprimento de onda? Justifique sua resposta.

(Capítulo 15.Exercícios – Exercícios 13) Uma onda transversal em uma corda possui amplitude de , comprimento de onda igual a e velocidade de . Ela é representada pela função dada no exercício 15.12. a) Para o tempo , calcule para intervalos de iguais a (ou seja, e assim por diante) desde até . Faça um gráfico dos resultados obtidos. Essa é a forma da corda para o tempo . b) Repita o cálculo para os mesmos intervalos de para o tempo e para o tempo . Faça um gráfico da forma da corda para esses tempos. Qual é o sentido de propagação da corda?

(Capítulo 15.Exercícios – Exercícios 33) As ondas estacionárias em um fio são descritas pela Equação (15.28), com , e . A extremidade esquerda do fio está no ponto . Calcule as distâncias entre a extremidade esquerda do fio e a) os nós da onda estacionária, b) os ventres da onda estacionária.

(Capítulo 15.Problemas – Exercícios 49) Uma onda transversal senoidal com amplitude igual a 2,5 mm e comprimento de onda igual a 1,8 m propaga-se com velocidade de 36,0 m/s da esquerda para a direita ao longo de uma corda esticada horizontal. Considere a origem na extremidade esquerda da corda sem perturbação. No tempo t=0 a extremidade esquerda está sobre a origem e se move de baixo para cima. a) Ache a frequência, a frequência angular e o numero de onda desta onda. b) Qual é a função que descreve a onda? c) Qual é a função para uma partícula na extremidade esquerda da corda? d) Qual é a função para uma partícula situada a 1,35 m à direita da origem? e) Qual é o modulo máximo da velocidade transversal de qualquer partícula da corda? f) Ache o deslocamento transversal e a velocidade transversal de uma partícula situada a 1,35 m à direita da origem para o tempo .

(Cap. 15. Problemas Desafiadores - Ex.82)Um escafandrista está suspenso abaixo da superfície do Lago Ness por um cabo preso a um barco na superfície do lago (Figura 15.40). O mergulhador e seus equipamentos possuem massa total de e ocupam um volume igual a . O cabo possui diâmetro igual a e a densidade linear . O mergulhador imagina que viu algo se movendo nas profundezas escuras do lago e sacode a extremidade do cabo , produzindo ondas transversais que sobem através do cabo para sinalizar a seus companheiros que estão no barco.

a) Qual é a tensão no cabo em sua extremidade inferior presa ao mergulhador? Não se esqueça de incluir a força de empuxo que a água (densidade igual a ) exerce sobre ele.

b) Calcule a tensão no cabo a uma distância acima do mergulhador. A força de empuxo que a água exerce sobre o cabo deve ser incluída.

c) A velocidade de propagação de uma transversal é dada por equação (15.13). Portanto, a velocidade varia ao longo do cabo, visto que a tensão não é constante. (Esta relação despreza a força de amortecimento que a água exerce sobre o cabo que se move.) Integre para achar o tempo que o primeiro sinal leva para atingir a superfície.

(Capítulo 15.Problemas – Exercícios 50) Uma onda transversal sobre uma corda é dada por a) Ache a amplitude, o período, a frequência, o comprimento de onda e a velocidade de propagação da onda. b) Faça um desenho da corda para os seguintes valores de : e . c) A onda está se deslocando no sentido ou no sentido ? d) A massa por unidade de comprimento da corda é igual a . Ache a tensão e) Ache a potência média transportada por essa onda.

(Cap.16.2 – Ex.6) Um grande terremoto com epicentro em Loma Pietra, na Califórnia, perto de São Francisco, ocorreu às da tarde, hora local, no dia de outubro de (em TUC, Tempo Universal Coordenado, ocorreu à no dia de outubro de ). As ondas sísmicas primárias (ondas ) de um terremoto são ondas longitudinais que se propagam na crosta terrestre. Ondas desse terremoto foram detectadas em Caracas, na Venezuela, à , TUC; em Kevo, na Finlândia, à , TUC; e em Viena, Áustria, à , TUC. As distâncias percorridas pelas ondas desde o epicentro em Loma Pietra foram de até Caracas, até Kevo e até Viena.

1. Use os tempos de chegada das ondas para calcular a velocidade média de propagação das ondas até essas três cidades. Como você explica eventuais diferenças entre essas velocidades médias?
2. A densidade média da crosta terrestre é igual a aproximadamente . Use esse valor para calcular o módulo de compressão da crosta terrestre ao longo da trajetória seguida pelas ondas até elas atingirem cada uma das três cidades. Como suas respostas se comparam com os módulos de compressão listados na tabela 11.1?

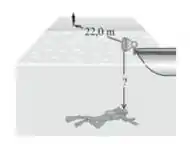
(Cap.16.2 – Ex. 7) Uma mergulhadora transportando uma scuba, que contém ar comprimido para respiração, escuta um som proveniente da buzina de um barco que está diretamente sobre ela na superfície de um lago. No mesmo instante, um amigo que está nas margens do lago a uma distância de da buzina também ouve o som da buzina. A buzina está a acima da superfície da água. Calcule a distância (indicada pelo ‘?’ na figura) entre a buzina e a mergulhadora. A temperatura do ar e da água é de .

(Cap.16- Ex. 9)Um oscilador vibrando a produz uma onda sonora que se desloca em um gás ideal a 325 m/s quando a temperatura do gás é . Em um certo experimento, você precisa que o mesmo oscilador produza um som de comprimento de onda igual a nesse gás. Qual deveria ser a temperatura do gás para obter esse comprimento de onda?

(Cap.16- Ex. 11)Um cabo de latão com de comprimento é golpeado em uma extremidade. Na outra extremidade, uma pessoa ouve dois sons vindos de duas ondas longitudinais, uma se deslocando no cabo metálico e a outra no ar. Qual é o intervalo de tempo entre os dois sons? A velocidade do som no ar é igual a ; as informações relevantes sobre o latão podem ser encontradas nas Tabelas 11.1 e 14.1.

(Cap.16- Ex.18)Qual é o nível da intensidade sonora no ouvido quando a intensidade do som é igual a ? b) Qual é o nível da intensidade sonora nas proximidades de um bate-estacas quando a amplitude de pressão do som é de e a temperatura é igual a ?

(Cap.16 - Ex.21)A boca de um bebê está a de distância do ouvido do pai e a do ouvido da mãe. Qual é a diferença entre o nível de intensidade do som ouvido pelo pai e o nível de intensidade do som ouvido pela mãe?

(Cap.16.4 – Ex. 24) A frequência fundamental de um tubo aberto em ambas as extremidades é . a) Qual é o comprimento desse tubo? Se agora fechamos uma extremidade, calcule b) o comprimento de onda e c) a nova frequência fundamental.

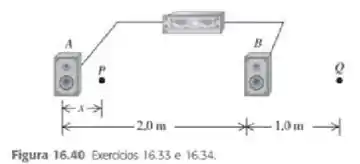
(Cap.16.6 – Ex. 33) Dois alto-falantes, A e B (Figura 16.40), são alimentados por um mesmo amplificador e emitem ondas senoidais em fase. O alto-falante B está a uma distância de à direita do alto-falante A. a velocidade do som no ar é igual a . Considere o ponto Q ao longo da extensão da linha reta que une os dois alto-falantes, situado a uma distância de à direita do alto-falante B. Os dois alto-falantes emitem ondas sonoras que se propagam diretamente dos alto-falantes até o ponto Q. a) Qual é a menor frequência capaz de produzir interferência construtiva no ponto Q? b) Qual é a menor frequência capaz de produzir interferência destrutiva no ponto Q?

(Cap.16.Exercícios – Ex. 44) Um trem se desloca com velocidade de com o ar calmo. A frequência da nota emitida pelo apito da locomotiva é igual a . Qual é o comprimento de onda das ondas sonoras: a) na parte frontal da locomotiva? b) atrás da locomotiva? Qual é a frequência do som que um ouvinte em repouso escuta quando ele está: c) na frente da locomotiva? d) atrás da locomotiva?

(Cap.16.Exercícios – Ex. 44) Um trem se desloca com velocidade de com o ar calmo. A frequência da nota emitida pelo apito da locomotiva é igual a . Qual é o comprimento de onda das ondas sonoras: a) na parte frontal da locomotiva? b) atrás da locomotiva? Qual é a frequência do som que um ouvinte em repouso escuta quando ele está: c) na frente da locomotiva? d) atrás da locomotiva?