Young – Física 2 termodinâmica e ondas – 12º edição – Capítulo 13, Problemas
(Cap 13- Ex 72) Um bloco de massa igual a está submetido a uma força restauradora elástica e a constante da força é igual a . Faça um gráfico da energia potencial em função do deslocamento no intervalo de até . Em seu gráfico, adote a escala no eixo vertical e no eixo horizontal. O bloco inicia o movimento oscilatório com uma energia potencial igual a e uma energia cinética igual a . Examinando o gráfico, responda às perguntas seguintes. Qual é a amplitude da oscilação? Qual é a energia potencial quando o deslocamento é igual a metade da amplitude? Para qual deslocamento a energia potencial é igual a igual a energia cinética? Qual é o valor do ângulo de fase , sabendo que a velocidade inicial é positiva e o deslocamento inicial é negativo?
Passo 1
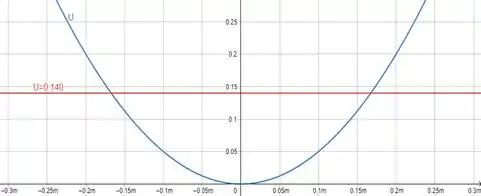
Para resolver o que o enunciado quer saber, precisamos fazer o gráfico que é pedido no item primeiro, então abaixo temos o gráfico o gráfico pedido.
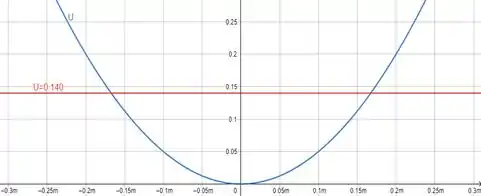
O enunciado nos diz que inicialmente temos que e , assim a energia mecânica inicial é dada por:
E como a energia mecânica se conserva temos esse valor a todo momento no movimento.
Passo 2
Para achar a amplitude olhando o gráfico como é pedido no enunciado, temos que nos atentar a algumas coisas.
A energia total também pode ser achada da seguinte maneira:
Que também é igual a energia potencial máxima que ocorre na amplitude, já que não temos energia cinética na amplitude do movimento.
Então se temos a energia potencial máxima igual a energia mecânica na amplitude, basta olharmos no gráfico em que ponto temos esse valor para , que no caso é no ponto
Passo 3
Quando o deslocamento é igual a metade da amplitude , temos um deslocamento
Olhando no gráfico, vemos que a energia potencial nesse ponto é de .
Passo 4
Agora temos que achar o deslocamento para o caso que , se temos e sabendo que:
Assim:
Agora temos que olhar no gráfico o ponto que isso acontece, só que no gráfico que o enunciado pediu não da para ter uma noção clara em que ponto isso acontece, assim temos que partir para álgebra.
Sabemos que:
E
E queremos o caso que , já que a outra metade está na forma de energia cinética, então temos o seguinte:
Então temos que:
Como sabemos que , temos:
Passo 5
Para achar o ângulo de fase pedido no item o melhor caminho é a álgebra mesmo, onde já temos uma equação para encontrar esse ângulo que é:
Onde e , são respectivamente a velocidade inicial e a posição inicial, que podemos achar com as fórmulas da energia cinética e potencial iniciais, respectivamente, já que esses valores são dados, temos então:
E
Isolando-as nas equações temos:
E
A posição é negativa e a velocidade é positiva pois o enunciado pede assim.
Temos também que , agora vamos substituir isso que encontramos a equação para achar .
Temos:
Simplificando, temos:
Substituindo e , temos:
Assim, temos que:
Resposta
