Física Termodinâmica e Ondas – Young e Freedman – 12 edição – Capítulo 13 – Exercício 4.
(Cap 13 - Ex 4) O deslocamento de um objeto oscilando em função do tempo é mostrado na Figura 13.30. Quais são (a) a frequência; (b) a amplitude; (c) o período; (d) a frequência angular desse movimento?
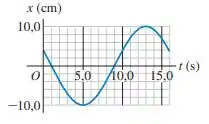
Passo 1
E ai xuxu’s tudo certinho?:
Bora lá?
Iremos calcular a frequência.
O período é o tempo de um ciclo e a amplitude é o deslocamento máximo do equilíbrio.
Ambos os valores podem ser lidos no gráfico.
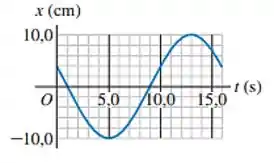
Bom pelo gráfico podemos ver que o objeto completou uma oscilação em 16 segundos. Cada fileira de quadradinhos, representa 1 segundo, portanto o período é 16 segundos, e como, por definição, a frequência é o inverso do período
Passo 2
Agora vamos para o item (b). A amplitude do movimento, designada por A, é o módulo máximo do vetor deslocamento do corpo a partir da posição de equilíbrio; isto é, o valor máximo de |x|. Ela é sempre positiva.
Logo a amplitude é
Passo 3
É a vez do item (c), o período. Mas... Esse a gente já calculou no passo 1 😊.
Só ressaltando
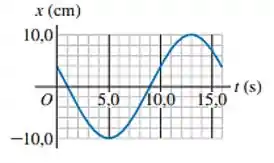
Pelo gráfico podemos ver que o objeto completou uma oscilação em 16 segundos. Cada fileira de quadradinhos, representa 1 segundo, portanto o período é 16 segundos.
Passo 4
Item (d) calcular a frequência angular, que por definição é
Então