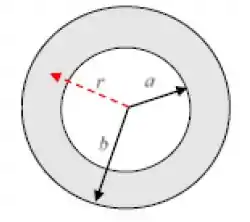
Uma coroa circular isolante, plana, com raio interno e raio externo ,possui uma quantidade total de carga . Esta carga é distribuída de maneira não uniforme sobre a coroa circular, de tal forma que a densidade superficial é dada por: , onde é uma constante positiva e é a distância do centro da coroa circular até qualquer ponto sobre ela, como mostrado na figura. Considere que o potencial é nulo no infinito ( no infinito).
- Calcule a carga total na coroa circular em função de e dos raios e .
- Calcule o potencial no centro da coroa circular, deixando a sua expressão em função de e dos outros dados do problema.
Passo 1
Fala galera, tudo bem? Vou ajudar você a resolver essa questão! Vamos lá?
Letra (a):
Vamos começar calculando o diferencial de carga:
O diferencial de área para essa figura é , agora é só substituir o diferencial de área e a expressão para a densidade superficial de carga e integrar de até :
Passo 2
Letra (b):
O diferencial de potencial é dado por:
Mas , assim para achar o potencial integramos de até :
No entanto, do passo anterior temos que a carga é , ou seja, podemos substituir o valor de daqui em termos da carga total e dos raios e :
Assim podemos substituir no potencial:
Podemos abrir o termo no produto e fazer algumas simplificações:
Beleza?
Pronto pra próxima questão? =)