PUCRIO – Física 3 2020.1 – G1– Questão 2
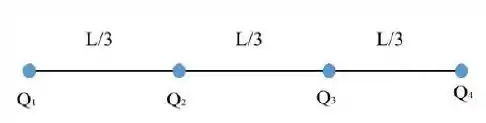
Quatro cargas e, estão fixadas em um segmento de reta de comprimento de reta, como mostra a figura.
- Calcule a energia potencial eletrostática total para o sistema das quatro cargas.
- Encontre e justifique o valor total da energia cinética para o sistema quando o tempo tende a infinito.
Suponha que as cargas sejam, na realidade, partículas de massas idênticas . No instante , todas as partículas estão em repouso, na configuração mostrada na figura. Nesse instante, as partículas são soltas (todas com velocidades nulas) e passam a se mover apenas sob a ação das forças eletrostáticas.
Passo 1
Fala galera, tudo bem? Vou ajudar você a resolver essa questão! Vamos lá?
Letra (a):
A energia potencial é:
Então teremos seis pares de partículas:
E a energia potencial total é a soma de todas as energias:
Tranquilo até aqui?
Passo 2
Letra (b):
Pelo teorema da conservação de energia temos:
Como (partem do repouso), (no infinito não temos interação eletrostática) e , então podemos calcular a energia cinética final do sistema :
Toda energia potencial é convertida em energia cinética.
Beleza?
Pronto pra próxima questão? =)