Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Introdução à Lei de Gauss

Ver Teoria
Exercício 31123456789101112131415161718192021222324252627282930

Enunciado

PUCRIO – Física 3 2020.1 – G1– Questão 4

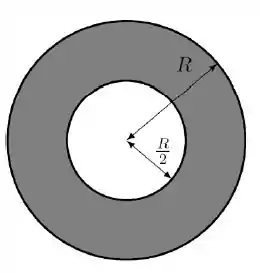
Uma casca esférica de raio interno R i = R / 2 e raio externo R e = R possui uma densidade volumétrica de carga esfericamente simétrica que obedece à relação ρ ( r ) = ρ 0 r / R , onde r é a distância entre o centro da esfera e o ponto de avaliação. Calcule o campo elétrico E ( r )   nas regiões:

  1. r < R / 2
  2. R 2 < r < R
  3. R < r

Passo 1

Fala galera, tudo bem? Vou ajudar você a resolver essa questão! Vamos lá?

Aqui vamos pensar primeiro na simetria esférica do problema! Em qualquer ponto desse sistema, a superfície gaussiana é uma esfera de raio r :

∮ E → ⋅ d A → = q i n t ϵ 0

E 4 π r 2 = q i n t ϵ 0

Então o problema fica encontrar a carga interna em cada superfície para cada região.

Para a região (i):

r < R / 2

E ali não temos carga, logo q i n t = 0 , assim o campo é nulo:

E r = 0

Passo 2

Agora na região (ii):

R 2 < r < R

A carga está distribuída uniformemente de acordo com a densidade superficial ρ 0 r / R :

q i n t = ∫ R 2 r ρ 0 r R 4 π r 2 d r = 4 ρ 0 π R r 4 4 R 2 r = ρ 0 π r 4 R - R 3 16

E aqui o campo elétrico é:

E 4 π r 2 = q i n t ϵ 0

E 4 π r 2 = ρ 0 π ϵ 0 r 4 R - R 3 16

E = ρ 0 4 ϵ 0 r 2 r 4 R - R 3 16

Passo 3

E agora na região (iii) temos que r > R e a carga interna será colocando r = R na expressão do passo anterior para a carga interna:

q i n t r = R = ρ 0 π ( R ) 4 R - R 3 16

q i n t = 15 16 π ρ 0 R 3

E o campo elétrico aqui é:

E 4 π r 2 = q i n t ϵ 0

E = 1 ϵ 0 . 15 16 . π ρ 0 R 3 . 1 4 π r 2  

E = 15 ρ 0 R 3 64 ϵ 0 r 2

Beleza?

Pronto pra próxima questão? =)

Resposta

e m   r < R 2 : E = 0

e m   R 2 < r < R : E = ρ 0 4 π ϵ 0 r 2 r 4 R - R 3 16

e m   r > R :   E = 15 ρ 0 R 3 64 ϵ 0 r 2

Exercícios de Livros Relacionados

Explique por que a intensidade do campo elétrico aumenta linearmente com r no lugar de decrescer com inverso de r 2 entre o centro e a superfície de uma esfera sólida carregada uniformemente.
Como as fórmulas para a lei da gravidade de Newton e para a lei de Coulomb têm a mesma dependência com o inverso do quadrado da distância, uma fórmula análoga à da lei da Gauss pode ser determinada pa
Uma casca uniformemente carregada com densidade volumétricaρ contém em seu interior uma cavidade esférica. Mostre que o campo no interior da cavidade é uniforme e é dado por E → = ρ d → 3 ϵ 0 , onde d
Qual é o fluxo elétrico através de um dos lados de um cubo que tem uma carga puntiforme isolada de - 3,00μ C colocada no seu centro? Dica: você não precisa integrar nenhuma equação para obter a respos
Medidas cuidadosas do campo elétrico na superfície de uma caixa preta indicam que o fluxo elétrico resultante saindo da superfície da caixa é 6,0k N ⋅ m 2 / C . (a) Qual é a carga resultante dentro da