Exercícios Resolvidos de Fluxo de Campo Elétrico

Exercício 39 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 40 41 42 43 44 45 46 47

Enunciado

PUCRIO – Física 3 2020.1 – G1– Questão 3

q = 5 n C ; e (b) uma esfera maciça isolante de raio, com carga total desconhecida, distribuída de maneira uniforme, conforme mostram as figuras. Ao traçarmos uma superfície Gaussiana fechada no formato de uma semiesfera de raio concêntrica com a esfera maciça, obtemos que o fluxo elétrico através dessa superfície é: . Encontre a densidade volumétrica de carga da esfera. (Nos cálculos, considere ).

Passo 1

Fala galera, tudo bem? Vou ajudar você a resolver essa questão! Vamos lá?

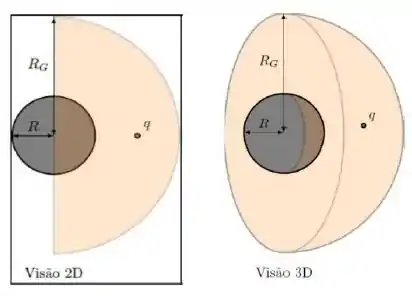
Dentro da superfície de Gauss estamos envolvendo a carga pontual e metade da esfera maciça de carga , então carga interna é:

Passo 2

Pela lei de Gauss, o fluxo elétrico é:

Então podemos calcular a carga :

Passo 3

E como a densidade é uniforme, podemos distribuir essa carga em todo volume da esfera de raio :

Beleza?

Pronto pra próxima questão? =)

Resposta

Exercícios de Livros Relacionados

15.8E As duas pequenas esferas metálicas vistas na Figura 15.16, de mesmo raio, estão suspensas por fios finos de náilon.Mostre que θ ' = θ . (B) Imagine que um fino fio condutor faça contato simultân

O fluxo de campo elétrico em cada face de um dado tem um valor absoluto, em unidades de 10 3 N · m 2 / C , igual ao número N de pontos da face ( 1 ⩽ N ⩽ 6 ). O fluxo é para dentro se N for ímpar e par

Um cubo possui arestas com comprimento L e é colocado com um dos vértices na origem, como indica a Figura 22.32 . O campo elétrico não é uniforme, porém é dado por E → = - B i ^ + C j ^ - D k ^ , onde

O campo elétrico E → 1 em uma das faces de um paralelepípedo é uniforme em todos os pontos dessa face e aponta perpendicularmente para fora da face. Na face oposta, o campo elétrico E → 2 também é uni

Uma superfície plana quadrada com lado igual a L é descrita pelas equações a Faça um desenho do quadrado e mostre os eixo x ,y e z . b Calcule o fluxo elétrico através do quadrado produzido por uma ca