PUCRIO – Física 3 2020.1 – G1– Questão 1
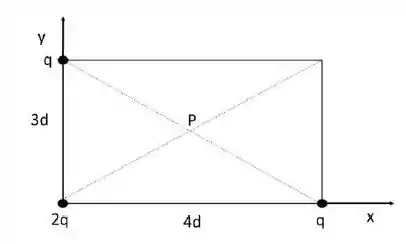
Três cargas, de valores estão colocadas nos vértices de um retângulo de lados e, como mostra a figura.
- Expresse as forças eletrostáticas vetoriais agindo nas partículas localizadas em , e .
- Uma partícula de carga é colocada na posição , que é o centro do retângulo. Calcule o módulo da força eletrostática devida ás três cargas sobre essa partícula.
Passo 1
Fala galera, tudo bem? Vou ajudar você a resolver essa questão! Vamos lá?
Para começar vamos calcular essa diagonal:
O ângulo de referência será o ângulo entre a diagonal e o eixo horizontal:
Agora podemos calcular as forças!
Letra (a):
Na partícula que está em temos duas forças: vertical pelo par com a carga e na direção da diagonal pelo par com a carga .
Lembrando que e , então:
Agora na partícula na origem temos uma componente vertical (que vem do par com a carga ) e outra horizontal (que vem do par com a carga ):
E na partícula na posição temos duas forças: uma na diagonal e outra na horizontal.
Tranquilo até aqui?
Passo 2
Letra (b):
O módulo da força é apenas o módulo da força entre e , pois as outras duas forças sobre a carga se cancelam, beleza?
Sendo assim, temos:
Beleza?
Pronto pra próxima questão? =)