PUCRIO – Física 3 2020.1 – G1– Questão 6
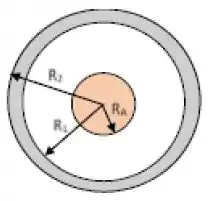
Uma casca esférica condutora de raio interno e raio externo é carregada com uma carga liquida positiva . No interior da casca é posicionada uma pequena esfera condutora, de raio , carregada com a mesma carga Considere que no infinito e que
- Determine as expressões do potencial elétrico nas regiões:
- Se uma carga igual a é transportada do infinito até ser depositada na casca esférica, calcule (utilizando os valores fornecidos), nesta nova condição, quais são as densidades de carga superficiais na superfície da esfera de raio e nas superfícies internas e externas da casca esférica.
Passo 1
Fala galera, tudo bem? Vou ajudar você a resolver essa questão! Vamos lá?
Letra (a):
O potencial é
A carga será ( da carga induzida e mais da carga líquida dentro da região), e , assim o potencial vale:
E para estamos dentro do condutor da casca esférica, assim temos um potencial que é igual aquele para , portanto:
Passo 2
Letra (b):
Na nova situação é alterada somente a carga na superfície externa da casca, então:
E temos apenas na superfície em . A densidade superficial de carga interna é:
E internamente, em , a carga é a mesma , mas com sinal negativo, daí a densidade fica:
E por fim externamente como não temos carga líquida, a densidade superficial é nula:
Beleza?
Pronto pra próxima questão? =)