PUCRIO – Física 3 2020.1 – G1– Questão 7
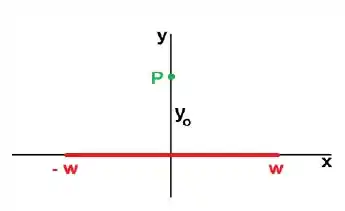
A fita cuja seção transversal está mostrada na Figura tem largura , espessura desprezível e comprimento infinito ao longo do eixo z. Está carregada com a densidade superficial de carga onde é constante e positiva .
- Inicialmente, determine uma expressão geral para o vetor campo elétrico devido a um fio infinito carregado com uma densidade linear de carga positiva (), observando seu módulo e sentido em cada ponto do espaço.
- Em seguida, considere que a fita pode ser decomposta em fios de espessuras infinitesimais. Finalmente, use o resultado do item anterior para determinar o vetor campo elétrico (módulo e sentido) devido à fita em um ponto de observação arbitrário do eixo situado acima dela e que dista da origem.
Passo 1
Fala galera, tudo bem? Vou ajudar você a resolver essa questão! Vamos lá?
Letra (a):
Vamos supor uma superfície gaussiana cilíndrica de raio , altura em torno no fio. O campo elétrico é:
E este campo é radial, ou seja, perpendicular ao fio em cada ponto de observação e se afasta dele.
Passo 2
Letra (b):
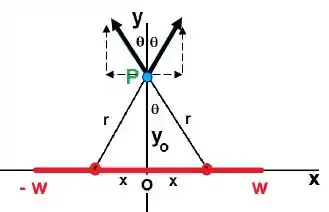Para essa combinação de fios, vamos precisar de um desenho para verificar a simetria do problema.
A figura acima mostra que a combinação de dois fios simétricos em relação à origem produz um campo no sentido . As componentes horizontais dos campos são canceladas, então apenas a componente do campo será considerada.
Lembrando que , o diferencial de campo é:
E agora vamos integrar de até , ou duas vezes de até (que é o que vou escolher, por simplicidade):
Beleza?
Pronto pra próxima questão? =)