P2 de Física 3 da USP - 2017

Um resistor circular de raio contido no plano e centrado na origem é feito de duas metades com resistências e . O resistor está ligado a um par de fios semi-infinitos que se estendem ao longo do eixo e que são percorridos por uma corrente , conforme a figura.

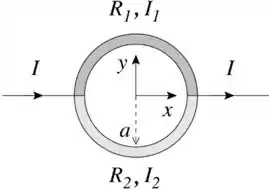
(a) Calcule o valor das correntes e que atravessam respectivamente os resistores e em função de , e . Indique o sentido de cada uma das correntes.

(b) Calcule o vetor campo magnético no centro do resistor circular.

Uma esfera condutora de raio está no interior de uma casca esférica fina condutora de raio . A esfera e a casca esférica são concêntricas e o espaço entre elas está preenchido com um material de resistividade constante, conforme a figura. Uma corrente elétrica , uniformemente distribuída através do material entre os condutores, flui da esfera interna para a casca esférica.

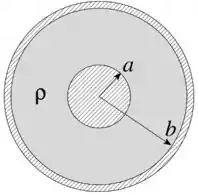
(a) Determine o vetor densidade de corrente na região entre os condutores ().

(b) Calcule a diferença de potencial entre os condutores.

(c) Calcule a resistência elétrica entre os condutores.

(d) Calcule a resistência entre os condutores no limite em que .

Uma espira quadrada de lado , contida no plano , é percorrida por uma corrente no sentido horário, conforme a figura. Na região onde se encontra a espira existe um campo magnético

onde é uma constante.

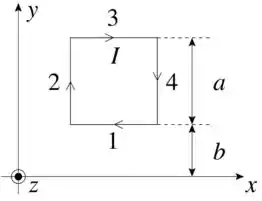
(a) Calcule a força magnética sobre os lados e da espira.

(b) Calcule a força magnética sobre os lados e da espira.

(c) Calcule a força resultante sobre a espira.

(I) Calcule o módulo do campo magnético produzido por um solenóide muito longo com espiras por unidade de comprimento, percorrido por uma corrente . Despreze efeitos de borda.

(II) Dois solenóides muito longos, coaxiais, cujos eixos coincidem com o eixo , transportam, cada um, uma corrente porém com sentidos opostos, como mostra a figura. O solenóide de raio tem espiras por unidade de comprimento e o de raio tem espiras por unidade de comprimento. Despreze efeitos de borda.

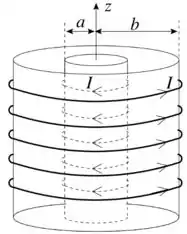
(a) Determine o vetor para .

(b) Determine o vetor para .

(c) Determine o vetor para .