Um resistor circular de raio contido no plano e centrado na origem é feito de duas metades com resistências e . O resistor está ligado a um par de fios semi-infinitos que se estendem ao longo do eixo e que são percorridos por uma corrente , conforme a figura.
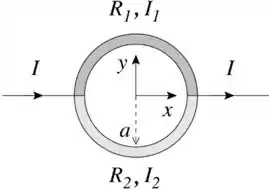
(a) Calcule o valor das correntes e que atravessam respectivamente os resistores e em função de , e . Indique o sentido de cada uma das correntes.
(b) Calcule o vetor campo magnético no centro do resistor circular.
Passo 1
Temos que os dois resistores estão associados em paralelo, ou seja, a diferença de potencial entre os dois é igual
Usando a lei de Ohm
Por outro lado, temos que a corrente se divide entre as correntes e
Usando essas duas relações encontramos que
Passo 2
Para calcular o campo no centro do resistor temos que usar a lei de Biot-Savart
lembrando que o vetor aponta da fonte de corrente até o ponto onde queremos calcular o campo magnético e que é um pedaço de curva por onde passa o campo.
No caso dos dois fios semi-infinitos, o vetor está na direção , assim como a direção da corrente (. Dessa forma o produto vetorial da lei de Biot-Savart, , será nulo.
Passo 3
No caso do resistor , a corrente passa ao longo do círculo no sentido horário, o que significa que , onde é o vetor unitário tangente ao círculo.
Como estamos lidando em coordenadas polares, temos que o elemento de arco será dado por
Já o vetor unitário , aponta de onde está a corrente para o ponto onde queremos calcular o campo. Nesse caso, esse vetor será dado por , ou seja, apontando para o centro do círculo.
Assim o produto vetorial será dado por
Outro jeito de visualizar a direção do campo magnético seria usar a regra da mão direita e vendo que o campo tem que apontar na direção que entra na folha (ou tablet, monitor, celular...), ou seja, .
Agora podemos calcular o campo! Como a corrente está sobre o círculo de raio , temos que
Passo 4
No caso do resistor , a corrente passa ao longo do círculo no sentido anti-horário, o que significa que , onde é o vetor unitário tangente ao círculo.
De novo teremos que , ou seja, apontando para o centro do círculo e
Assim o produto vetorial será dado por
Outro jeito de visualizar a direção do campo magnético seria usar a regra da mão direita e vendo que o campo tem que apontar na direção que sai da folha (ou tablet, monitor, celular...), ou seja, .
Passo 5
O campo total será a soma dos campos
Em termos das resistências e