Uma espira quadrada de lado , contida no plano , é percorrida por uma corrente no sentido horário, conforme a figura. Na região onde se encontra a espira existe um campo magnético
onde é uma constante.
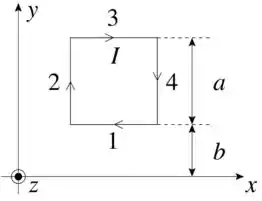
(a) Calcule a força magnética sobre os lados e da espira.
(b) Calcule a força magnética sobre os lados e da espira.
(c) Calcule a força resultante sobre a espira.
Passo 1
Quando o campo magnético e a direção da corrente em um fio são constantes temos que a força magnética sobre esse fio será
Sobre o lado da espira temos que o campo magnético é constante e .
A corrente que passa por esse lado é orientada na direção e percorre uma distância , de forma que a força sobre este lado será
Passo 2
Sobre o lado 3 da espira temos que o campo magnético é constante e .
A corrente que passa por esse lado é orientada na direção e percorre uma distância , de forma que a força sobre este lado será
Passo 3
Sobre os lados e temos que o campo magnético varia ao longo do caminho da corrente (direção ). Nesse caso teremos que olhar o diferencial de força
No caso do fio temos que a corrente está indo na direção , começando em e terminando em . A força atuando em um pedaço desse fio será
De modo que
Passo 4
No caso do fio temos que a corrente está indo na direção . O procedimento é o mesmo que no caso do fio , porém com uma corrente indo na direção oposta. Dessa forma temos que a força no fio será a mesma que no fio em magnitude, mas no sentido oposto, ou seja
Passo 5
A força total sobre a espira será a soma de todas as forças que já calculamos
Resposta
- ,
- ,