(I) Calcule o módulo do campo magnético produzido por um solenóide muito longo com espiras por unidade de comprimento, percorrido por uma corrente . Despreze efeitos de borda.
(II) Dois solenóides muito longos, coaxiais, cujos eixos coincidem com o eixo , transportam, cada um, uma corrente porém com sentidos opostos, como mostra a figura. O solenóide de raio tem espiras por unidade de comprimento e o de raio tem espiras por unidade de comprimento. Despreze efeitos de borda.
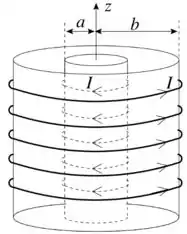
(a) Determine o vetor para .
(b) Determine o vetor para .
(c) Determine o vetor para .
Passo 1
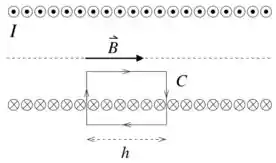
Para calcular o campo magnético gerado pelo solenóide, temos que usar a lei de Ampère. Fora do solenóide o campo será nulo e dentro será uniforme.
Escolhendo o caminho , indicado na figura, temos que a corrente total passando pelo seu interior é , onde é a largura da nossa Amperiana.
Passo 2
Agora temos que analisar o campo magnético produzido por dois solenoides diferentes em regiões. Para facilitar a vida vamos olhar cada um dos solenóides de forma separada. Já sabemos que em um solenóide o campo é dentro e nulo fora do solenóide.
- Solenóide menor (raio )
O módulo do campo magnético será e ele apontará para a direção (pela regra da mão direita)
- Solenóide maior (raio )
O módulo do campo magnético será e ele apontará para a direção (pela regra da mão direita)
Agora podemos fazer nossas análises!
Passo 3
Na região teremos contribuição dos dois solenóides
Passo 4
Na região teremos contribuição somente do solenóide maior
Passo 5
Na região não teremos nenhuma contribuição dos solenóides
Resposta
II)a)
II)b)
II)c)