P3 de Física 3 da USP - 2010

Um solenoide longo de comprimento , seção reta circular de raio e com espiras é percorrido por uma corrente . O módulo do campo magnético no interior solenoide é dado por .

Calcule o vetor campo elétrico no interior do solenoide.

Calcule o vetor campo elétrico fora do solenoide.

Uma bobina toroidal de raio interno e seção reta quadrada de lado , com , possui espiras percorridas por uma corrente .

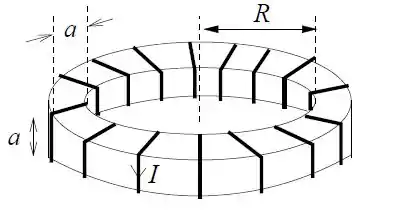
Calcule o vetor campo magnético no interior do toróide.

Calcule a autoindutância da bobina supondo que o módulo do campo magnético seja aproximadamente constante dentro da bobina.

Suponha que a bobina toroidal seja preenchida com um núcleo de um material magnético com permeabilidade magnética relativa . Calcule os novos valores do vetor campo magnético no seu interior e da autoindutância.

Considere um fio infinito percorrido por uma corrente estacionária . Coplanar com o fio está uma espira retangular de lados e e resistência . A distância da espira ao fio infinito é D, conforme a figura.

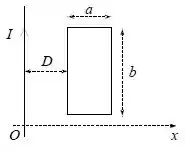
Dado: O módulo do campo magnético produzido por um fio infinito num ponto a uma distância do fio é .

Calcule o fluxo magnético sobre a área da espira.

Calcule a mútua indutância do sistema fio-espira.

Suponha que a espira é deslocada com velocidade constante paralelamente ao fio. Calcule o valor da corrente na espira.

Suponha que a espira é afastada do fio com velocidade na direção perpendicular a esse fio. Calcule a força eletromotriz induzida e a corrente na espira no instante em que a distância da espira ao fio é . Determine o sentido da corrente induzida (horário ou anti-horário), justificando sua resposta.

Um solenoide de autoindutância é percorrido por uma corrente estacionária .

Qual é o valor da energia magnética armazenada no indutor?

Por meio de um chaveamento, no instante , o indutor é colocado em série com um capacitor de capacitância de modo a formar um circuito . A corrente inicial no indutor é e a carga inicial no capacitor é . Use a lei de conservação de energia para determinar a carga máxima que pode ser atingida no capacitor.

Escreva a equação diferencial para a carga do capacitor e determine a frequência angular de oscilação .