Considere um fio infinito percorrido por uma corrente estacionária . Coplanar com o fio está uma espira retangular de lados e e resistência . A distância da espira ao fio infinito é D, conforme a figura.
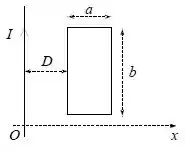
Dado: O módulo do campo magnético produzido por um fio infinito num ponto a uma distância do fio é .
Calcule o fluxo magnético sobre a área da espira.
Calcule a mútua indutância do sistema fio-espira.
Suponha que a espira é deslocada com velocidade constante paralelamente ao fio. Calcule o valor da corrente na espira.
Suponha que a espira é afastada do fio com velocidade na direção perpendicular a esse fio. Calcule a força eletromotriz induzida e a corrente na espira no instante em que a distância da espira ao fio é . Determine o sentido da corrente induzida (horário ou anti-horário), justificando sua resposta.
Passo 1
Calcule o fluxo magnético sobre a área da espira.
Por definição, o fluxo magnético é dado por:
O problema já nos disse que o campo magnético a uma distância do fio é
Assim, como o campo magnético varia apenas com a distância do fio, o elemento será
Onde
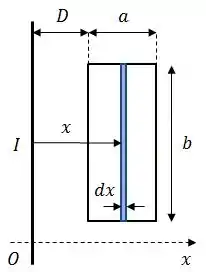
Voltando para a expressão do fluxo magnético, teremos:
Integrando esse cara, teremos:
Passo 2
Calcule a mútua indutância do sistema fio-espira.
Por definição, a indutância mútua entre duas espiras é dada por:
Nesse caso, a indutância mútua será dada por:
Obs: Como não temos mais de um enrolamento na espira, .
Substituindo a expressão de que calculamos no item anterior, teremos:
Passo 3
Suponha que a espira é deslocada com velocidade constante paralelamente ao fio. Calcule o valor da corrente na espira.
Para que surja uma corrente induzida, é necessário que apareça uma induzida. A induzida é determinada pela Lei de Faraday, dada por:
Entretanto, como a espira está sendo deslocada paralelamente ao fio, não há variação do fluxo magnético, que só aconteceria se a espira estivesse se deslocando perpendicularmente ao fio.
Logo:
Finalmente:
Passo 4
Suponha que a espira é afastada do fio com velocidade na direção perpendicular a esse fio. Calcule a força eletromotriz induzida e a corrente na espira no instante em que a distância da espira ao fio é . Determine o sentido da corrente induzida (horário ou anti-horário), justificando sua resposta.
Agora sim, podemos começar a conversar.
Como dissemos anteriormente, a induzida será dada por:
Então vamos começar escrevendo a expressão do fluxo magnético na espira. A expressão é a mesma que calculamos na letra , a única diferença é que, ao invés de , a distância entre o fio e a espira será . Logo:
Ajeitando esse cara, teremos:
Agora sim! A induzida será dada por:
Passo 5
A corrente induzida será dada por:
Substituindo a expressão de que acabamos de calcular, teremos:
Passo 6
Para determinar o sentido da corrente induzida, vamos ter que recorrer à Lei de Lenz, que diz que:
O sentido de qualquer efeito de indução magnética é tal que ele se opõe à causa que produz esse efeito.
Mas basicamente o que nós precisamos tirar disso é que:
Se o fluxo do campo magnético está aumentando, o campo induzido tenta atrapalhar ele. Se o fluxo está diminuindo, o campo induzido tenta ajudar ele.
Ok! O fluxo do campo magnético é dado por:
O campo magnético está entrando na página, portanto.
Como :
Como o fluxo do campo magnético está diminuindo, o campo induzido vai tentar ajuda-lo, logo, deve estar na mesma direção e sentido do campo magnético gerado pelo fio na espira.
Como o campo gerado pelo fio na espira está entrando na página, o campo magnético induzido deve estar entrando na página também.
Para que a corrente induzida gere um campo entrando na página, ela deve estar no sentido horário.
Resposta
A corrente induzida está no sentido horário.