Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Lei de Lenz

Ver Teoria
Exercício 44123456789101112131415161718192021222324252627282930313233343536373839404142434546474849505152535455565758596061626364656667686970717273747576777879808182838485868788899091929394959697

Enunciado

Lei de Faraday, Potencial Elétrico

Um solenoide longo de comprimento L , seção reta circular de raio a ≪ L e com N espiras é percorrido por uma corrente I = I 0 cos ⁡ ω t . O módulo do campo magnético no interior solenoide é dado por B = μ 0 N I / L .

a ) Calcule o vetor campo elétrico no interior do solenoide.

b ) Calcule o vetor campo elétrico fora do solenoide.

Passo 1

a ) Calcule o vetor campo elétrico no interior do solenoide.

Pra começar, precisamos lembrar que:

ε = ∮ C E → ∙ d l →

Devido a geometria cilíndrica do problema, podemos dar uma simplificada na expressão acima:

ε = E r 2 π r → E r = ε 2 π r

Agora, para calcular a f e m , vamos ter que recorrer à Lei de Faraday:

ε = - ∂ ϕ B ∂ t = - ∂ ∂ t ∫ S B → ∙ d A →

Lembrando que:

B → r = μ 0 N I L ,     r < a 0 ,     r > a

Passo 2

  • r < a :

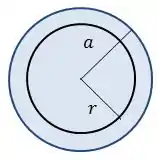
    • Nesse caso:

    B r = μ 0 N I L = μ 0 N I 0 L cos ⁡ ω t

    Como o campo magnético é uniforme, podemos dar uma simplificada na Lei de Faraday:

    ε = - ∂ ∂ t B A

    Onde A = π r 2 , logo:

    ε = - ∂ ∂ t μ 0 N I 0 L cos ⁡ ω t π r 2

    ε = - μ 0 N I 0 π r 2 L ∂ ∂ t cos ⁡ ω t

    ε = μ 0 ω N I 0 π r 2 sen ⁡ ω t L

    Portanto, o campo magnético será dado por:

    E r = ε 2 π r = μ 0 ω N I 0 π r 2 sen ⁡ ω t 2 π r L

    E r = μ 0 ω N I 0 r sen ⁡ ω t 2 L

    Finalmente:

    E → r = μ 0 ω N I 0 r sen ⁡ ω t 2 L ϕ ^  

    Passo 3

    b ) Calcule o vetor campo elétrico fora do solenoide.

  • r > a

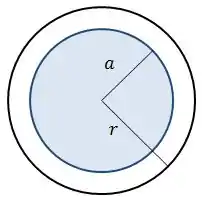
Nesse caso, como B r = 0 para r > a , o fluxo magnético será dado por:

ϕ B = B π a 2

Já que é somente pela circunferência de raio a que passa o campo magnético, logo:

ε = - ∂ ∂ t B π a 2

ε = - ∂ ∂ t μ 0 N I 0 L cos ⁡ ω t π a 2

ε = - μ 0 N I 0 π a 2 L ∂ ∂ t cos ⁡ ω t

ε = μ 0 ω N I 0 π a 2 sen ⁡ ω t L

Portanto, o campo magnético será dado por:

E r = ε 2 π r = μ 0 ω N I 0 π a 2 sen ⁡ ω t 2 π r L

E r = μ 0 ω N I 0 a 2 sen ⁡ ω t 2 r L

Finalmente:

E → r = μ 0 ω N I 0 a 2 sen ⁡ ω t 2 r L ϕ ^  

Resposta

a )

E → r = μ 0 ω N I 0 r sen ⁡ ω t 2 L ϕ ^

b )

E → r = μ 0 ω N I 0 a 2 sen ⁡ ω t 2 r L ϕ ^

Exercícios de Livros Relacionados

20- Uma barra metálica com 1.50m de comprimento é puxada para a direita a 5.0m / s regulares e perpendicularmente a um campo magnético uniforme de 0.750T . A barra desliza sobre trilhos metálicos para
17- Use a lei de Lenz para determinar o sentido da corrente induzida que passa no resistor a b indicado na Figura 29.33 , quando ( a ) a chave S é aberta depois de ficar fechada durante alguns minutos
15- Um anel circular está em uma região do espaço onde existe um campo magnético uniforme, como indica a Figura 29.31 . O campo magnético está entrando no plano da figura. Determine o sentido (horário
18- Um tubo de papelão é circundado por dois enrolamentos feitos com dois fios isolados, formando espiras em sentidos contrários, como indica a Figura 29.34 . Os terminais a e b do enrolamento A podem
16- A corrente na Figura 29.32 obedece a equação I t = I 0 e - b t . Em que b0 . Determine o sentido (horário ou anti-horário) da corrente induzida na bobina redonda para t0 .