Lei de Ampère, Indutância, Materiais Magnéticos
Uma bobina toroidal de raio interno e seção reta quadrada de lado , com , possui espiras percorridas por uma corrente .
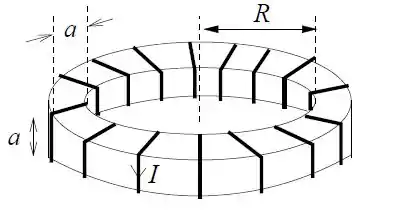
Calcule o vetor campo magnético no interior do toróide.
Calcule a autoindutância da bobina supondo que o módulo do campo magnético seja aproximadamente constante dentro da bobina.
Suponha que a bobina toroidal seja preenchida com um núcleo de um material magnético com permeabilidade magnética relativa . Calcule os novos valores do vetor campo magnético no seu interior e da autoindutância.
Passo 1
Calcule o vetor campo magnético no interior do toróide.
Esse é um problema clássico de Lei de Ampère, dada por:
Como queremos calcular o campo magnético no interior do toróide, a nossa amperiana será uma circunferência de raio , centrada no eixo da bobina. Assim, podemos simplificar a Lei de Ampère para:
Nesse caso, a corrente será , logo:
A julgar pelo sentido corrente , o campo magnético está no sentido anti-horário, logo:
Passo 2
Calcule a autoindutância da bobina supondo que o módulo do campo magnético seja aproximadamente constante dentro da bobina.
Por definição, a autoindutância de uma bobina é dada por:
Onde é o fluxo magnético. Como o campo magnético é constante e uniforme, será dado por:
Onde é a área da seção transversal quadrada da bobina.
Portanto, a autoindutância será:
Passo 3
Suponha que a bobina toroidal seja preenchida com um núcleo de um material magnético com permeabilidade magnética relativa . Calcule os novos valores do vetor campo magnético no seu interior e da autoindutância.
Quando o núcleo da bobina é preenchida com material magnético, de permeabilidade magnética , para determinar o campo magnético, basta substituir por na expressão que calculamos anteriormente:
Logo:
O mesmo vale para autoindutância:
Resposta