P3 de Física 3 da USP - 2011

Um solenoide longo de comprimento e raio tem um enrolamento com espiras.

Calcule a autoindutância do solenoide. Calcule a energia armazenada no solenoide quando pelo fio circula uma corrente .

Dado: o campo magnético no interior do solenoide é . Ignore a variação do campo próximo às extremidades do solenoide.

Repita os cálculos do item (a) para o caso em que o solenoide está preenchido com um material de suscetibilidade .

O campo magnético em todos os pontos de uma região cilíndrica de raio é uniforme e direcionado para dentro da página, variando com o tempo segundo , onde é uma constante positiva.

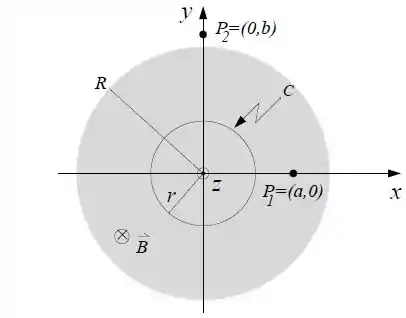
Determine a circulação do campo elétrico, , ao longo do círculo de raio mostrado na figura, percorrido no sentido anti-horário.

Determine o vetor campo elétrico (módulo, direção e sentido) nos pontos e da figura, onde e .

O circuito mostrado na figura 1 contém um resistor e um indutor em série com uma bateria de fem . A chave está inicialmente fechada e, portanto, nenhuma corrente passa pelo resistor , conforme a figura 1.

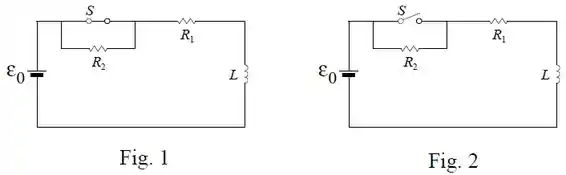
Se a chave permaneceu fechada por um tempo muito longo antes de , qual é a corrente estacionária no circuito antes da abertura da chave?

Com a corrente percorrendo o circuito, a chave é aberta no instante , de forma que uma nova resistência é adicionada em série aos demais elementos (veja a figura 2). Escreva equação diferencial para que descreve o comportamento do circuito para . Qual é a corrente no circuito imediatamente após a abertura da chave?

Imediatamente após a abertura da chave, calcule a força eletromotriz induzida pela variação de fluxo magnético através do indutor. Expresse sua resposta somente em termos de , e .

Uma barra condutora perfeita (com resistência nula) desliza sem atrito com velocidade , para a esquerda, sobre dois fios condutores também perfeitos. Dois resistores e estão conectados às extremidades dos dois fios, formando o circuito mostrado na figura. A distância entre os fios horizontais é , entre os resistores é , e da barra ao resistor é . Um campo magnético uniforme e constante de intensidade é aplicado perpendicularmente ao circuito, para fora da página. Ao calcular o fluxo magnético através de qualquer superfície, adote o vetor normal à superfície, na mesma direção e sentido do campo magnético.

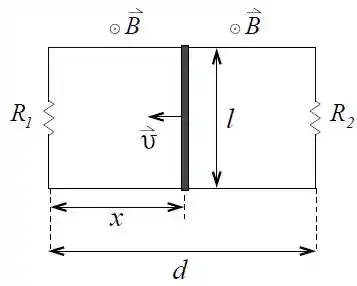
Determine o sentido (horário ou anti-horário) da corrente na porção do circuito à direita da barra justificando a sua resposta por meio da Lei de Lenz.

Calcule o fluxo magnético através da porção do circuito à direita da barra. Determine a corrente que atravessa o resistor por meio da Lei de Faraday.

Determine o sentido (horário ou anti-horário) da corrente na porção do circuito à esquerda da barra justificando a sua resposta por meio da Lei de Lenz.

Calcule o fluxo magnético através da porção do circuito à esquerda da barra. Determine a corrente que atravessa o resistor por meio da Lei de Faraday.

Calcule a intensidade e a direção da força magnética exercida sobre a barra. Essa força é de aceleração ou de frenagem?