O circuito mostrado na figura 1 contém um resistor e um indutor em série com uma bateria de fem . A chave está inicialmente fechada e, portanto, nenhuma corrente passa pelo resistor , conforme a figura 1.
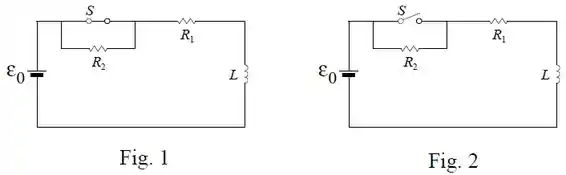
Se a chave permaneceu fechada por um tempo muito longo antes de , qual é a corrente estacionária no circuito antes da abertura da chave?
Com a corrente percorrendo o circuito, a chave é aberta no instante , de forma que uma nova resistência é adicionada em série aos demais elementos (veja a figura 2). Escreva equação diferencial para que descreve o comportamento do circuito para . Qual é a corrente no circuito imediatamente após a abertura da chave?
Imediatamente após a abertura da chave, calcule a força eletromotriz induzida pela variação de fluxo magnético através do indutor. Expresse sua resposta somente em termos de , e .
Passo 1
Se a chave permaneceu fechada por um tempo muito longo antes de , qual é a corrente estacionária no circuito antes da abertura da chave?
Enquanto a chave permanece fechada, a corrente no circuito é dada por:
Quando dizemos que a chave permanece dessa forma por uma longo tempo, estamos dizendo que .
E quando o tempo tende ao infinito, a equação acima nos dá a seguinte corrente:
Passo 2
Com a corrente percorrendo o circuito, a chave é aberta no instante , de forma que uma nova resistência é adicionada em série aos demais elementos (veja a figura 2). Escreva equação diferencial para que descreve o comportamento do circuito para . Qual é a corrente no circuito imediatamente após a abertura da chave?
Quando a chave é aberta, a resistência total do circuito passa a ser . Logo, através da Lei das Malhas, teremos:
Passo 3
Imediatamente após a abertura da chave, calcule a força eletromotriz induzida pela variação de fluxo magnético através do indutor. Expresse sua resposta somente em termos de , e .
A força eletromotriz induzida no indutor é dada por:
Substituindo isso na equação diferencial que encontramos na letra , teremos:
Imediatamente após a abertura da chave, devido aos efeitos inerciais do indutor, a corrente ainda é igual a , logo:
Onde .
Finalmente:
Resposta