O campo magnético em todos os pontos de uma região cilíndrica de raio é uniforme e direcionado para dentro da página, variando com o tempo segundo , onde é uma constante positiva.
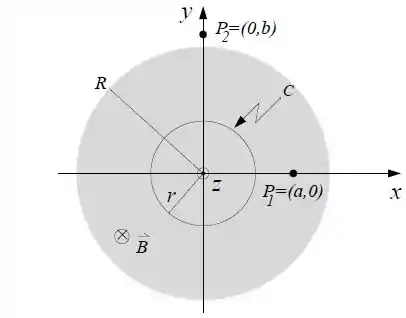
Determine a circulação do campo elétrico, , ao longo do círculo de raio mostrado na figura, percorrido no sentido anti-horário.
Determine o vetor campo elétrico (módulo, direção e sentido) nos pontos e da figura, onde e .
Passo 1
Determine a circulação do campo elétrico, , ao longo do círculo de raio mostrado na figura, percorrido no sentido anti-horário.
A circulação do campo elétrico, pedida pelo problema será justamente a fem induzida, que é determinada pela Lei de Faraday:
O fluxo magnético é dado por:
Como o campo magnético está entrando no plano da página:
Substituindo isso na expressão de , teremos:
Logo:
Passo 2
Determine o vetor campo elétrico (módulo, direção e sentido) nos pontos e da figura, onde e .
Na letra , encontramos que:
Por conta da simetria, tanto quando deve estar na direção .
Agora, o nosso trabalho aqui é aplicar isso a cada caso:
Como , teremos:
Como está na direção , no ponto , o campo vai apontar no sentido , logo:
Nesse caso, como :
Como está na direção , no ponto , o campo vai apontar no sentido , logo:
Resposta