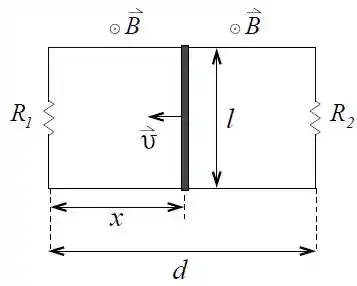
Uma barra condutora perfeita (com resistência nula) desliza sem atrito com velocidade , para a esquerda, sobre dois fios condutores também perfeitos. Dois resistores e estão conectados às extremidades dos dois fios, formando o circuito mostrado na figura. A distância entre os fios horizontais é , entre os resistores é , e da barra ao resistor é . Um campo magnético uniforme e constante de intensidade é aplicado perpendicularmente ao circuito, para fora da página. Ao calcular o fluxo magnético através de qualquer superfície, adote o vetor normal à superfície, na mesma direção e sentido do campo magnético.
Determine o sentido (horário ou anti-horário) da corrente na porção do circuito à direita da barra justificando a sua resposta por meio da Lei de Lenz.
Calcule o fluxo magnético através da porção do circuito à direita da barra. Determine a corrente que atravessa o resistor por meio da Lei de Faraday.
Determine o sentido (horário ou anti-horário) da corrente na porção do circuito à esquerda da barra justificando a sua resposta por meio da Lei de Lenz.
Calcule o fluxo magnético através da porção do circuito à esquerda da barra. Determine a corrente que atravessa o resistor por meio da Lei de Faraday.
Calcule a intensidade e a direção da força magnética exercida sobre a barra. Essa força é de aceleração ou de frenagem?
Passo 1
Determine o sentido (horário ou anti-horário) da corrente na porção do circuito à direita da barra justificando a sua resposta por meio da Lei de Lenz.
A Lei de Lenz diz que:
O sentido de qualquer efeito de indução magnética é tal que ele se opõe à causa que produz esse efeito.
Mas basicamente o que nós precisamos tirar disso é que:
Se o fluxo do campo magnético está aumentando, o campo induzido tenta atrapalhar ele (corrente no sentido horário). Se o fluxo está diminuindo, o campo induzido tenta ajudar ele (corrente no sentido anti-horário).
Ok! O fluxo do campo magnético é dado por (no caso de um campo magnético uniforme):
O campo magnético é constante e está saindo da folha, portanto, ele é positivo.
Como a área está aumentando, isso faz com que a variação da área com o tempo seja positiva:
Logo:
Opa! Como o fluxo do campo magnético está aumentando, a corrente estará no sentido horário.
Passo 2
Calcule o fluxo magnético através da porção do circuito à direita da barra. Determine a corrente que atravessa o resistor por meio da Lei de Faraday.
Por definição, o fluxo magnético é dado por:
Como o campo magnético é uniforme e constante, podemos simplificar essa expressão para:
Onde é a área da porção à direita da barra, dada por:
Portanto:
Passo 3
A Lei de Faraday é dada por:
Então, basta substituir a expressão de que acabamos de calcular:
Como está diminuindo com o tempo .
Pra determinar a corrente, basta usar a Lei de Ohm:
Passo 4
Determine o sentido (horário ou anti-horário) da corrente na porção do circuito à esquerda da barra justificando a sua resposta por meio da Lei de Lenz.
A variação do campo magnético é dada por.
Nesse caso, como a área está diminuindo, isso faz com que a variação da área com o tempo seja negativa:
Logo:
Como o fluxo do campo magnético está diminuindo, a corrente estará no sentido anti-horário.
Passo 5
Calcule o fluxo magnético através da porção do circuito à esquerda da barra. Determine a corrente que atravessa o resistor por meio da Lei de Faraday.
Novamente, o fluxo magnético será dado por:
Onde é a área da porção à esquerda da barra, dada por:
Portanto:
Passo 6
Novamente, a Lei de Faraday é dada por:
Substituindo a expressão de que acabamos de calcular, teremos:
Novamente, como diminui com o tempo , logo:
Assim, a corrente será dada por:
Passo 7
Calcule a intensidade e a direção da força magnética exercida sobre a barra. Essa força é de aceleração ou de frenagem?
A força magnética sobre um condutor retilíneo é dada por:
Como o problema apenas pede a intensidade da força magnética, teremos:
Sobre a barra, tanto a corrente quanto a corrente fluem de baixo para cima, logo, a corrente total sobre a barra é:
Portanto, a força magnética será:
Como a corrente flui de baixo para cima e o campo magnético está saindo da página, o produto vetorial apontará da esquerda para a direita.
Portanto, a força magnética aponta da esquerda para a direita. Sendo assim, é força de frenagem.
Resposta
A corrente estará no sentido horário.
A corrente estará no sentido anti-horário
A força magnética aponta da esquerda para a direita. Sendo assim, é força de frenagem.