P3 de Física 3 da USP - 2014
Física 3 - USP
Um solenoide longo de comprimento e raio tem um enrolamento com espiras. O módulo do campo no interior do solenoide é .
- Calcule a auto-indutância do solenoide.
- Repita o cálculo do item (a) para o caso em que o solenoide está preenchido com um material de suscetibilidade .
O circuito abaixo ficou durante um longo tempo com a chave fechada. No instante , a chave é aberta.
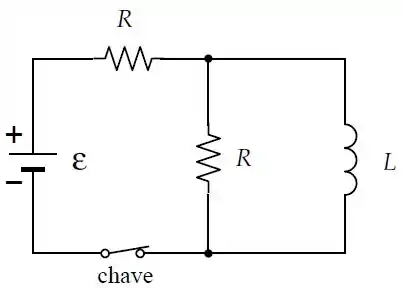
- Determine o valor da corrente através do indutor no instante em que a chave é aberta.
- Obtenha a equação diferencial para a corrente através do indutor para e determine a solução satisfazendo a condição inicial .
- Determine a energia total dissipada por efeito Joule no resistor para .
Se você não resolver o item (a), deixe os itens (b) e (c) em função de .
Uma espira quadrada de lado e resistência está sobre uma mesa, a uma distância de um fio muito longo sobre o eixo que transporta uma corrente , conforme mostra a figura. O módulo do campo produzido pelo fio é , onde é a distância até o fio.
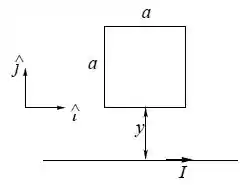
- Calcule o fluxo do campo magnético, produzido pelo fio através da espira.
- A espira é movimentada na direção , afastando-se do fio com velocidade . Use a lei de Lenz para determinar o sentido da corrente induzida na espira (horário ou anti-horário), justificando sua resposta. Calcule a corrente induzida .
- Determine o valor da corrente induzida se a espira é movimentada para a direita (direção ) mantendo constante a distância até o fio.
O campo magnético em todos os pontos de uma região cilíndrica de raio é uniforme e direcionado para dentro da página , variando com o tempo segundo , onde é uma constante positiva.
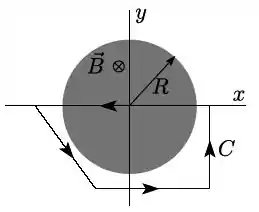
- Determine a integral do campo elétrico ao longo do circuito indicado na figura.
- Determine o vetor campo elétrico fora da região cilíndrica de raio .
- Determine o vetor campo elétrico dentro da região cilíndrica de raio .