Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Circuitos RL

Ver Teoria
Exercício 131234567891011121415161718192021222324252627282930313233343536373839404142434445464748495051525354

Enunciado

Circuito RL

O circuito abaixo ficou durante um longo tempo com a chave fechada. No instante t = 0 , a chave é aberta.

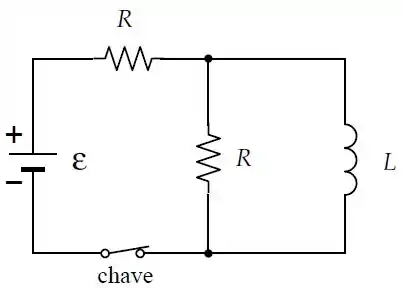
  1. Determine o valor da corrente I 0 através do indutor no instante t = 0 em que a chave é aberta.

    2. Se você não resolver o item (a), deixe os itens (b) e (c) em função de I 0 .

  2. Obtenha a equação diferencial para a corrente I t através do indutor para t > 0 e determine a solução satisfazendo a condição inicial I 0 = I 0 .
  3. Determine a energia total dissipada por efeito Joule no resistor para t > 0 .

Passo 1

  1. Determine o valor da corrente I 0 através do indutor no instante t = 0 em que a chave é aberta.

    2. Como o circuito ficou muito tempo com a chave fechada, ele está no regime estacionário.

    Nesse caso, a ddp no indutor é nula. A consequência disso é que toda a corrente que chega no ponto 1 “decide” ir pelo ramo do indutor, e não passa nenhuma corrente pelo resistor em paralelo com o indutor.

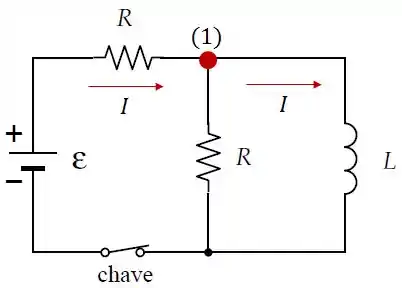
    Logo, a corrente no indutor enquanto a chave está fechada é:

    I = ε R

    Quando a chave é repentinamente aberta, não ocorre uma mudança descontínua de corrente no indutor... logo, assim que a chave é aberta em t = 0 , a corrente é a mesma.

    I 0 = ε R

    Passo 2

  2. Obtenha a equação diferencial para a corrente I t através do indutor para t > 0 e determine a solução satisfazendo a condição inicial I 0 = I 0 .

    3. t > 0 significa que a chave já está aberta... assim, não vai passar mais corrente pelo 1.

    A corrente agora só passará pelo indutor e pelo resistor 2.

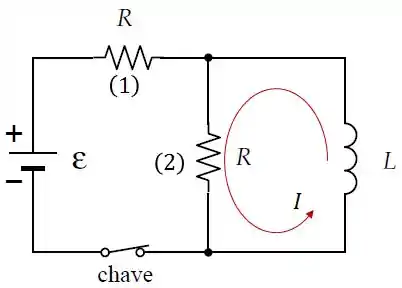
    Sabemos que a soma das ddps de qualquer malha deve ser nula... logo:

    V I + V R = 0

    L d I t d t + R I t = 0

    Agora vamos ter que resolver essa equação diferencial.

    Passo 3

    L d I t d t + R I t = 0

    Como se trata de uma EDO de primeira ordem separável... vamos ter que separar! (surpreendente, né?!)

    Agora a parada é mais braçal!

    L d I t d t = - R I t

    d I t I t = - R L d t

    ∫ I 0 I t d I t I t = - R L ∫ 0 t d t

    ln ⁡ I t I 0 = - R L t

    Lembrando que a constante de tempo indutiva é dada por:

    τ L = L R

    Substituindo isso na equação:

    ln ⁡ I t I 0 = - t τ L

    I t I 0 = e - t τ L

    I t = I 0 e - t τ L

    Passo 4

  3. Determine a energia total dissipada por efeito Joule no resistor para t > 0 .

Aqui basta você lembrar que a energia armazenada em um indutor é dada por:

U = 1 2 L I 2

Inicialmente, quando t = 0 → I 0 = I 0 . Nesse instante o indutor possui corrente máxima, logo, energia máxima.

Depois que a chave é aberta, a corrente vai diminuindo, logo, a energia vai diminuindo. Isso acontece porque a energia fornecida pelo indutor é dissipada pelo resistor.

Logo, a energia total dissipada pelo resistor é:

U = 1 2 L I 0 2

Resposta

  1. I 0 = ε R

  2. I t = I 0 e - t τ L

1 2 L I 0 2

Exercícios de Livros Relacionados

Quanto tempo é necessário, depois que a fonta é removida, para que a diferença de potencial entre os terminais do resistor de um circuito RL com L = 2,00H e R = 3,00Ω diminua para 10,0 % do valor inic
Um gerador de frequência ajustável é ligado em série com um indutor L = 2,50m H e um capacitor C = 3,00μ F . Para que frequência o gerador uma corrente com a maior amplitude possível no circuito?
A força eletromotriz da fonte do circuito da Fig. 30-16 varia com o tempo de tal forma que a corrente é dada por i t = 3,0 + 5,0 t , onde i está em ampères e t em segundos. Suponha que R = 4,0Ω e L =
Na Fig. 30-70, depois que a chave S é fechada no instante t = 0 , a força eletromotriz da fonte é ajustada automaticamente para manter uma corrente constante i passando pela chave. (a) Determine a cor
Na figura 30-73a, a chave S permaneceu na posição A por um tempo suficiente para que a corrente no indutor de indutância L 1 = 5,00m H e o resistor de resistência R 1 = 25,0Ω se estabilizasse. Da mesm