O campo magnético em todos os pontos de uma região cilíndrica de raio é uniforme e direcionado para dentro da página , variando com o tempo segundo , onde é uma constante positiva.
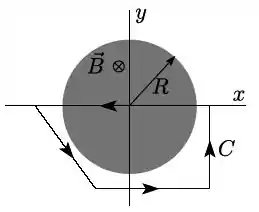
- Determine a integral do campo elétrico ao longo do circuito indicado na figura.
- Determine o vetor campo elétrico fora da região cilíndrica de raio .
- Determine o vetor campo elétrico dentro da região cilíndrica de raio .
Passo 1
- Determine a integral do campo elétrico ao longo do circuito indicado na figura.
- Determine o vetor campo elétrico fora da região cilíndrica de raio .
- Determine o vetor campo elétrico dentro da região cilíndrica de raio .
Essa integral que o problema pediu pra calcularmos na verdade é a definição de Lei de Faraday, seliga:
Esse é o fluxo do campo magnético pela área do circuito.
A área por onde o campo magnético passa por dentro do circuito será igual à metade da circunferência... conseguiu ver? E como não depende da área:
Ah! Lembrando que esse sinal negativo aparece porque o campo magnético está entrando na folha. Se estivesse saindo, o fluxo do campo magnético seria positivo.
Voltando para aquela integral:
Passo 2
Vamos de novo pela Lei de Faraday:
Beleza, como estamos querendo calcular o campo elétrico fora de região cilíndrica, a nossa curva será uma circunferência de raio :
Aqui vai acontecer a mesma coisa que na letra (a), a diferença é que agora a região em que estamos interessados é a circunferência inteira. Logo:
Mas po, beleza! Só não sei a direção do campo elétrico... mas se olharmos novamente para a Lei de Faraday:
Só de olhar a fórmula, vemos que o campo elétrico deve estar na direção do elemento , isso significa que o campo elétrico vai estar sempre na direção:
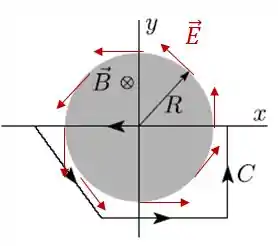
Portando:
Passo 3
Beleza! Essa é quase igual à letra (b), então o raciocínio é o mesmo.
A diferença agora é que a área atravessada pelo campo magnético será e a curva por onde passa o campo elétrico será . Onde .
Para o vetor campo elétrico vai acontecer a mesma coisa que o caso anterior, logo: