Uma espira quadrada de lado e resistência está sobre uma mesa, a uma distância de um fio muito longo sobre o eixo que transporta uma corrente , conforme mostra a figura. O módulo do campo produzido pelo fio é , onde é a distância até o fio.
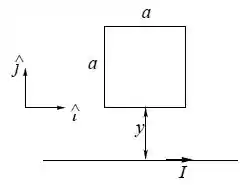
- Calcule o fluxo do campo magnético, produzido pelo fio através da espira.
- A espira é movimentada na direção , afastando-se do fio com velocidade . Use a lei de Lenz para determinar o sentido da corrente induzida na espira (horário ou anti-horário), justificando sua resposta. Calcule a corrente induzida .
- Determine o valor da corrente induzida se a espira é movimentada para a direita (direção ) mantendo constante a distância até o fio.
Passo 1
- Calcule o fluxo do campo magnético, produzido pelo fio através da espira.
- A espira é movimentada na direção , afastando-se do fio com velocidade . Use a lei de Lenz para determinar o sentido da corrente induzida na espira (horário ou anti-horário), justificando sua resposta. Calcule a corrente induzida .
- Determine o valor da corrente induzida se a espira é movimentada para a direita (direção ) mantendo constante a distância até o fio.
Vambora! O fluxo magnético é dado por:
Onde . Então o primeiro trabalho aqui vai ser calcular o campo magnético gerado pelo fio, certo?
(Ah! Coloquei ao invés de só pra diferenciar mesmo, porque a própria figura já usa um , tá vendo?)
Se bem que nem vai dar tanto trabalho, porque a Lei de Ampère diz que:
Nesse caso, vou considerar como curva uma circunferência de raio cujo centro é o próprio fio. Logo:
Por fim, usando a regra da mão direita, vemos que o o campo magnético que passa pela espira é:
Agora sim podemos calcular o fluxo magnético.
Passo 2
Já sabemos que:
Agora é correr pro abraço!
Por fim:
Passo 3
A Lei de Lenz diz que:
O sentido de qualquer efeito de indução magnética é tal que ele se opõe à causa que produz esse efeito.
Mas basicamente o que nós precisamos interpretar disso é que:
Se o fluxo do campo magnético está aumentando o campo induzido tenta atrapalhar ele (corrente no sentido horário). Se o fluxo está diminuindo o campo induzido tenta ajudar ele (corrente no sentido anti-horário).
Ok! O problema está falando que a espira está se afastando do fio de corrente .
Como vimos antes, o campo elétrico gerado pelo fio é dado por:
Então, se o valor de aumenta, significa que o campo magnético está diminuindo, certo?
Se o campo magnético está diminuindo, o fluxo do campo magnético também está diminuindo. Isso significa que o campo induzido tenta ajudar ele.
Logo, a corrente está no sentido anti-horário.
Passo 4
Pra calcular a corrente induzida, basta usar a Lei de Faraday... vamos usá-la pra calcular a fem induzida.
Lembrando que, segundo o enunciado, .
Passo 5
Agora é só calcular a corrente:
Passo 6
Nós já tínhamos visto que o campo magnético é dado por:
Bom, ele não depende de , certo? Isso significa que, se movermos a espira apenas na direção , o campo magnético permanece constante... logo: