P1 de Probest da UFRJ - 2014.2

Por saber que há uma grade procura por imóveis em determinada região muito valorizada, uma construtora decide comprar um terreno e construir uma casa nesse local.

1. O valor de venda desse imóvel depois de pronto pode também ser considerado como uma variável aleatória, com distribuição Normal, cuja média é milhão de reais. Qual deve ser o desvio padrão dessa distribuição para que se possa garantir, com de probabilidade, que a construtora conseguirá vender a casa por pelo menos mil reais?

Por saber que há uma grade procura por imóveis em determinada região muito valorizada, uma construtora decide comprar um terreno e construir uma casa nesse local.

b) O prazo necessário para realizar a obra pode ser encarado como uma variável aleatória com distribuição Exponencial. Com base na sua experiência, a construtora presume que uma obra como essa levaria em média meses para ficar pronta. Que prazo para entrega das chaves, a partir do início da obra, deve ser informado aos possíveis interessados na compra da casa? Admita que a construtora deseja ser capaz de cumprir esse prazo com de probabilidade.

Por saber que há uma grande procura por imóveis em determinada região muito valorizada, uma construtora decide comprar um terreno e construir uma casa nesse local.

1. Uma parte dos recursos necessários para isso será obtida através de um financiamento. Especialmente, admita que o percentual do gasto total a ser financiado se comporta como uma variável aleatória com distribuição Uniforme entre e . Qual é o coeficiente de variação dessa variável?

Três companhias aéreas servem uma pequena cidade no estado de São Paulo. As companhias , e tem, respectivamente e de voos programados. As taxas de voos que saem no horário programado são e , respectivamente.

1. Um voo acaba de sair no horário programado. Qual é a probabilidade que seja da companhia ?
2. Qual é a probabilidade de um voo não ser da companhia ou não sair no horário programado?

Três bolas enumeradas e estão num balde. Sorteamos duas bolas com reposição, e somamos os valores obtidos. Seja este valor.

1. Obter a função de probabilidade, a esperança e a variância de .
2. Refazer o item a) se as bolas forem sorteadas sem reposição.
3. Em ambos os casos, desenhar a função de distribuição acumulada de .

Considere a distribuição conjunta das variáveis aleatórias e , parcialmente dada pela seguinte tabela:

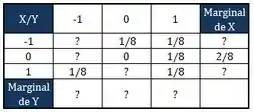
1. Sabendo que , complete a tabela.
2. Calcule e .
3. As variáveis e são independentes?
4. Quando um exemplo pode ser usado para se mostrar que uma afirmação do tipo (SE... ENTÃO...) é falsa então dizemos que ele é um contra-exemplo para essa afirmação. Os itens anteriores constituem um contra-exemplo para que afirmação falsa?