P1 de Probest da UFRJ - 2012.1

Em um curso secundário, dos estudantes são do sexo masculino e dos estudantes são do sexo feminino. Entre os rapazes, 20% estudam ciências, enquanto entre as moças, apenas 10% dedicam-se às ciências. Obtenha as probabilidades de que:

1. um estudante escolhido ao acaso estude ciências;
2. um estudante de ciências selecionado ao acaso seja do sexo feminino.

O valor exato de uma certa grandeza, expresso em uma unidade apropriada, é igual a , onde . Quando essa grandeza é medida com o uso de um determinado instrumento, o resultado da medição se comporta como uma variável aleatória , que segue uma distribuição . O erro relativo correspondente a essa medição é . A probabilidade de que esse erro relativo seja maior que 0,5 é igual a 0,02.

1. Qual é o valor de , se ?
2. Qual é o valor de , se ?

Obs.: Nesta questão os cálculos devem ser efetuados sempre com duas casas decimais.

Sabe-se que ocorre, em média, um acidente por dia numa certa estrada. Além disso, o número de ocorrências de acidentes ao longo de um intervalo de tempo de duração fixa segue uma distribuição de Poisson. Calcular a probabilidade de que:

1. num determinado dia ocorressem pelo menos 3 acidentes. (calcule o resultado com 2 casas decimais);
2. num grupo de 4 dias houvesse exatamente 2 dias, dos 4 selecionados, com pelo menos 3 acidentes por dia.

Obs.: Para simplificar os seus cálculos, use nas contas os valores (aproximados) que constam na tabela abaixo:

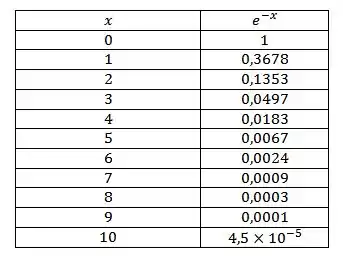
Seja a velocidade, medida em m/s, de um objeto de massa em movimento retilíneo. Suponha que é uma variável aleatória contínua com densidade

1. Calcule o valor esperado da energia cinética .
2. O objeto permanece com velocidade durante 8 segundos, percorrendo metros. Calcule a variância de .

Uma urna contém 3 bolas brancas e 2 bolas vermelhas. Um experimento consiste em se extrair sequencialmente e sem reposição duas bolas e registrar suas cores. Seja a v.a. que representa o número de bolas brancas retiradas nas duas extrações e seja a v.a. que assume 1 se a primeira bola extraída é branca e 0 se a primeira bola extraída é vermelha.

1. Obtenha a distribuição conjunta de e através de uma tabela e diga se e são independentes, justificando. Sugestão: Na montagem da tabela, comece determinando as distribuições marginais de e de . Em seguida, obtenha e . Finalmente complete a tabela, respeitando as propriedades de uma distribuição conjunta.
2. Calcule a covariância de e .