Três companhias aéreas servem uma pequena cidade no estado de São Paulo. As companhias , e tem, respectivamente e de voos programados. As taxas de voos que saem no horário programado são e , respectivamente.

1. Um voo acaba de sair no horário programado. Qual é a probabilidade que seja da companhia ?
2. Qual é a probabilidade de um voo não ser da companhia ou não sair no horário programado?

(a)

Temos que calcular a probabilidade do voo ser da empresa sabendo que ele acaba de sair no horário programado, que é o mesmo que:

Isso tem cara de que pra você? Bayes, probabilidade total? Bayes! Concorda comigo que a gente já sabe de uma informação meio que “futura” (que o voo saiu no horário programado) e a gente precisa dizer a probabilidade desse voo ser da empresa ? Isso é a cara de Bayes. Sempre que tiver algo assim, é Bayes.

Usando a fórmula de Bayes:

Como sempre, a gente vai ter que usar a probabilidade total pra poder calcular , que é a probabilidade total do voo sair no horário programado, sendo ele da empresa ou .

Substituindo todos esses valores que a gente já conhece:

Agora a gente já tem tudo que a gente precisa pra achar a resposta desse item:

(b)

Primeiro vamos ver qual é a notação pra isso...

O que a gente quer é a probabilidade de acontecer um ou outro, ou seja, da união desses dois eventos:

Tá, como que a gente vai resolver isso?

Pensa comigo... a gente tem dois eventos (vou mostrar naqueles diagramas porque fica bem mais fácil pra entender).

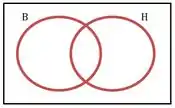
A gente que unir tudo que não tá em com tudo que não tá em .

Tudo que não tá em :

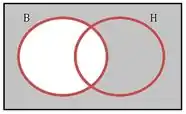
Tudo que não tá em :

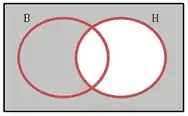
Unindo as duas fica assim:

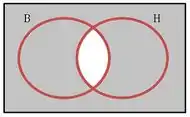
Beleza? É a probabilidade disso que a gente tem que calcular.

Com isso a gente pode dizer que:

Concorda? A probabilidade total é , e a probabilidade que a gente quer é menos a probabilidade da interseção dos eventos (que é aquele pedaço ali do meio, não pintado).

E o valor de a gente conhece, é só usar probabilidade condicional:

Então:

Agora é só resolver: