Considere a distribuição conjunta das variáveis aleatórias e , parcialmente dada pela seguinte tabela:
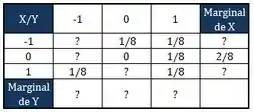
- Sabendo que , complete a tabela.
- Calcule e .
- As variáveis e são independentes?
- Quando um exemplo pode ser usado para se mostrar que uma afirmação do tipo (SE... ENTÃO...) é falsa então dizemos que ele é um contra-exemplo para essa afirmação. Os itens anteriores constituem um contra-exemplo para que afirmação falsa?
Passo 1
Tem uns espaços da tabela que a gente consegue completar automático, sem nem usar a informação do item (a). Vamos começar completando eles então.
Lembra que a soma de cada linha dá o valor da última coluna (marginal de ), e a soma das colunas dá a última linha (marginal de ) e que a somando a marginal de ou a marginal de , ambas tem que dar .
Sabendo disso, pensa comigo...
A gente pode começar somando a coluna do e achando o valor da marginal de .
Também podemos descobrir esse da linha do .
E a gente viu que o último quadradinho ali é .
Passo 2
Nossa tabela passa a ficar assim:
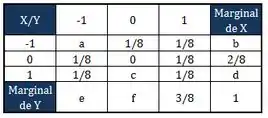
Aproveitei pra chamar os outros pontos de interrogação de incógnitas, pra facilitar nossa vida.
Agora vamos a luta.
Passo 3
(a)
Esse item diz que e pede pra completar a tabela.
Vamos usar probabilidade condicional pra abrir isso aí.
E a gente conhece esses dois dados aí.
é da coluna da marginal de .
E é só cruzar a linha do com a coluna do .
Então a gente tem que:
Mas isso ainda não significa nada pra gente, porque a gente não conhece nem e nem . A gente precisa de uma outra equação entre essas incógnitas.
Passo 4
Vamos achar outra relação entre elas então.
Se você reparar, e estão na mesma linha, isso nos dá uma outra relação, concorda? É só fazer a soma da linha.
Passo 5
Vamos juntar as duas equações.
Substitui a primeira na segunda:
Agora volta na primeira:
Passo 6
Tá, agora a gente vai achar todas as outras, só somando linhas e colunas.
Se a gente conhece , podemos conhecer .
Passo 7
Se a gente conhece , podemos conhecer .
Passo 8
Conhecendo , conhecemos .
Passo 9
Pra fechar, sabendo , a gente acha o .
A tabela completa fica assim:
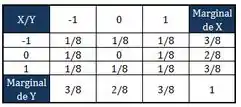
Passo 10
(b)
Vamos calcular as esperanças de e de . Pra fazer isso é só a gente multiplicar os possíveis valores de cada um pelas suas respectivas probabilidades. Os possíveis valores dos dois são os mesmos: . E as probabilidades de cada um a gente tira das marginais. Desse jeito:
Passo 11
Já pra fazer a esperança das duas juntas, , a gente multiplica todos os valores de por todos os de e pelas suas interseções, que são os valores de dentro da nossa tabela.
Pegou a ideia? É meio que sair multiplicando geral, cruzando as linhas com as colunas.
Fazendo essa conta doida aí, fica:
Passo 12
Pra fechar, a covariância, que é dada pela fórmula:
Foi?
Passo 13
(c)
Qual o critério pras variáveis serem independentes?
Certo? Então a gente tem que verificar se isso é verdade pra todos os casos na nossa tabela.
e no caso seriam nossos e que estão nas marginais e a interseção ali, , seria nosso que são os valores do interior da tabela.
A gente tem que procurar um exemplo que não obedeça ao critério, que aí já podemos dizer que não são independentes.
Óh:
Vamos verificar se isso é verdade, pela tabela:
Visivelmente não é verdade, beleza? Então as variáveis não são independentes.
Passo 14
(d)
Os itens anteriores nos dizem uns dados importantes. Primeiro a gente tem que as variáveis não são correlacionadas já que:
E ao mesmo tempo a gente sabe que elas não são independentes!
Mas pera! Se e são independentes então eles não são correlacionados, justo? Se duas variáveis não dependem uma da outra então elas não se relacionam.
Só que é exatamente isso que a gente não tem na questão haha... aqui a gente tem duas variáveis que não são independentes e ao mesmo tempo não são correlacionadas. Duas variáveis que dependem uma de outra, mas não se correlacionam.
Então:
“Se e são independentes então e são não correlecionadas” é uma verdade, maaas, sua recíproca não é verdadeira.