Determine a solução da inequação no intervalo .
Passo 1
Primeiramente, vamos determinar onde o cosseno atinge os valores extremos do intervalo. Por tabela:
E:
Passo 2
Mas algo que eu recomendo fazer pra não se confundir é usar o círculo trigonométrico:
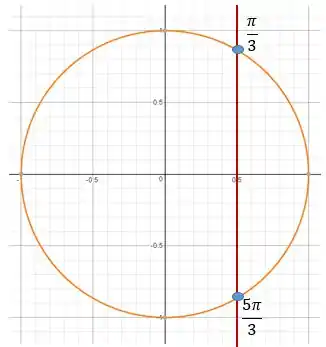
Queremos todos os à direita dessa reta, ou seja:
Resposta
Exercícios de Livros Relacionados
Use os gráficos de f e g e o método da adição gráfica para esboçar os gráficos de f + g . f x = x , g x = 1 / x
Prove que, se 0xπ 2 , então s e nx+c o sx1 Sugestão: ciclo trigonométrico e desigualdade triangular.
Para que valores de t existe x satisfazendo a igualdade cos x =t + 2 2 t - 1?
Sendo s e n alpha = (2)/(3) , com 0api , calcule cos ((pi)/(4) + alpha)
Sabendo que s e n x = (15)/(17) , s e n y = - (3)/(5) , 0x(pi)/(2) e piy(3 pi)/(2) , calcule s e n ( x + y ) , c o s ( x + y ) e t g ( x + y ) .