USP, Sem Campus, Cálculo 1, Listas de C1 - Profº Fernando Manfio - Lista 4, Questão 9
Prove que existe tal que
para .
Passo 1
Oiie, tudo bem?
Temos que analisar a seguinte desigualdade
e, então avaliar se existe , tal que . Vamos tentar reescrever um pouco esta desigualdade! Saca só!
Passo 2
Se somarmos em toda a desigualdade temos que
O gráfico das duas funções são tais que
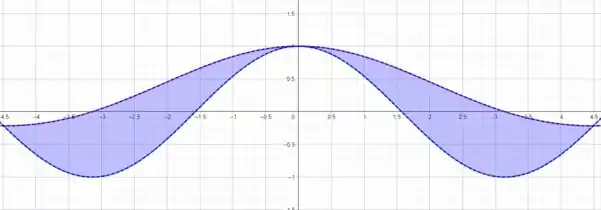
em que a curva superior é , note que temos que ambas têm o mesmo valor, lembre que
o valor da interseção exata é muito complicado de se obter, mas, note que precisamos apenas mostrar que para um a relação é verdade, e isso é válido para qualquer , por exemplo
em que
E, assim por diante, a questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
Ao longo dos passos!
Exercícios de Livros Relacionados
Use os gráficos de f e g e o método da adição gráfica para esboçar os gráficos de f + g . f x = x , g x = 1 / x
Prove que, se 0xπ 2 , então s e nx+c o sx1 Sugestão: ciclo trigonométrico e desigualdade triangular.
Para que valores de t existe x satisfazendo a igualdade cos x =t + 2 2 t - 1?
Sendo s e n alpha = (2)/(3) , com 0api , calcule cos ((pi)/(4) + alpha)
Sabendo que s e n x = (15)/(17) , s e n y = - (3)/(5) , 0x(pi)/(2) e piy(3 pi)/(2) , calcule s e n ( x + y ) , c o s ( x + y ) e t g ( x + y ) .