Exercícios Resolvidos de Intensidade de Radiação

Exercício 2 1 3 4 5 6 7 8

Enunciado

De acordo com a sua distribuição direcional, a radiação solar que incide sobre a superfície terrestre pode ser dividida em duas parcelas. A parcela direta, que é constituída por raios paralelos que incidem em um ângulo fixo , e a parcela difusa, formada por radiação que pode ser aproximada como sendo distribuída de forma difusa em relação a .

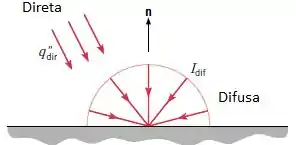
Considere condições de céu claro nas quais a radiação direta incide com um ângulo , com um fluxo total (baseado na área normal aos raios) de , e a intensidade total de radiação difusa é de .

Qual é o valor da irradiação solar total na superfície terrestre?

Passo 1

A irradiação total é dada pela somas das irradiações direta e difusa, logo:

A irradiação direta é dada por:

Enquanto a irradiação difusa é dada por:

Portanto:

Passo 2

Substituindo os valores:

Resposta

Exercícios de Livros Relacionados

Quando a variação da quantidade de radiação espectral com comprimento de onda é conhecida, como é determinada a quantidade total correspondente?

Considere que a intensidade da radiação solar incidente sobre a superfície terrestre pode ser expressa como I i = 100 cos ⁡ θ , onde I i tem as unidades de W / m 2 . s r . Determine o valor de pico da

Uma pequena superfície de área emite radiação como um corpo negro a T 1 = 1000K . Um detector de radiação ( A 2 ) é colocado à direção normal de visualização da superfície A 1 , a distância L, como mo

Considere uma abertura de 10m m de diâmetro onde a radiação é emitida como um corpo negro com poder emissivo de 2,87 × 10 - 5W / m ² ². O sensor de radiação é posicionado com 30 ° de inclinação fora d

Uma pequena superfície de área A = 1c m ² ² é submetida a uma radiação incidente de intensidade constante I i = 2,2 × 10 4W / m 2 . s r ao longo de todo hemisfério. Determine a taxa em que a energia d