(Adaptado) Uma pequena fonte de calor radiante com área emite difusamente com uma intensidade . Uma segunda área pequena, está localizada como mostrado no esboço a seguir.
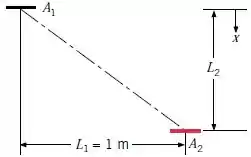
Determine a irradiação de para .
Passo 1
A irradiação de é dada por:
Onde a taxa de calor que sai da fornalha e atinge o sensor é dada por:
Como as áreas são muito menores que a distância entre elas, o ângulo sólido pode ser calculado da seguinte forma:
Dessa forma, a irradiação será dada por:
Passo 2
Onde:
Dessa forma, a irradiação será:
![]()