Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Intensidade de Radiação

Ver Teoria
Exercício 71234568

Enunciado

A distribuição espectral da radiação emitida por uma superfície difusa pode ser aproximada como segue.

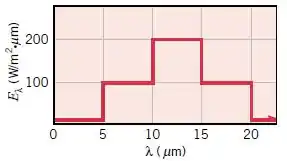
a Qual é o poder emissivo total?

b Qual é a intensidade total da radiação emitida na direção normal e em um ângulo de 30 ° em relação à normal?

c Determine a fração do poder emissivo total deixando a superfície nas direções π / 4 ≤ θ ≤ π / 2 .

Passo 1

a Qual é o poder emissivo total?

Como o problema está nos dando a distribuição em função de comprimentos de onda, o poder emissivo total será dado por:

E = ∫ 0 ∞ E λ . d λ

E = ∫ 0 5 0 d λ + ∫ 5 10 100 d λ + ∫ 1 0 1 5 200 d λ + ∫ 15 20 100 d λ + ∫ 2 0 ∞ 0 d λ

E = 100 × 10 - 5 + 200 × 15 - 10 + 100 × 20 - 15

Passo 2

b Qual é a intensidade total da radiação emitida na direção normal?

Tratando a superfície como difusa, a intensidade de radiação será dada por:

I e = E π = 2000 π

Passo 3

c Determine a fração do poder emissivo total deixando a superfície nas direções π / 4 ≤ θ ≤ π / 2 .

O que estamos querendo calcular aqui é:

E π 4 → π 2 E = ∫ ϕ = 0 2 π ∫ θ = π / 4 π / 2 I e . cos ⁡ θ . sen ⁡ θ . d θ . d ϕ π I e

Como a intensidade de radiação é constante:

E π 4 → π 2 E = ∫ ϕ = 0 2 π ∫ θ = π / 4 π / 2 cos ⁡ θ . sen ⁡ θ . d θ . d ϕ π

As integrais podem ser separadas em:

E π 4 → π 2 E = ∫ ϕ = 0 2 π d ϕ . ∫ θ = π / 4 π / 2 cos ⁡ θ . sen ⁡ θ . d θ π

Onde a primeira integral será igual a 2 π e a segunda integral pode ser resolvida por substituição, onde:

u = sen ⁡ θ → d u = cos ⁡ θ d θ

Dessa forma:

E π 4 → π 2 E = 2 π . ∫ u . d u π

E π 4 → π 2 E = 2 . u 2 2 = u 2 = sen 2 ⁡ θ π / 4 π / 2

E π 4 → π 2 E = 1 2 - 2 2 2

Resposta

a E = 2000   W / m 2

b I e = 637   W / ( m 2 . s r )

c E π 4 → π 2 / E = 0,5

Exercícios de Livros Relacionados

Quando a variação da quantidade de radiação espectral com comprimento de onda é conhecida, como é determinada a quantidade total correspondente?
Considere que a intensidade da radiação solar incidente sobre a superfície terrestre pode ser expressa como I i = 100 cos ⁡ θ , onde I i tem as unidades de W / m 2 . s r . Determine o valor de pico da
Uma pequena superfície de área emite radiação como um corpo negro a T 1 = 1000K . Um detector de radiação ( A 2 ) é colocado à direção normal de visualização da superfície A 1 , a distância L, como mo
Considere uma abertura de 10m m de diâmetro onde a radiação é emitida como um corpo negro com poder emissivo de 2,87 × 10 - 5W / m ² ². O sensor de radiação é posicionado com 30 ° de inclinação fora d
Uma pequena superfície de área A = 1c m ² ² é submetida a uma radiação incidente de intensidade constante I i = 2,2 × 10 4W / m 2 . s r ao longo de todo hemisfério. Determine a taxa em que a energia d