(Adaptado) Durante o tratamento térmico por radiação de um material na forma de uma fina película hemisférica é mantida por uma pressão de ar relativamente baixa. A irradiação sobre a película é devida à emissão de um aquecedor radiante com área , que emite de forma difusa com uma intensidade .
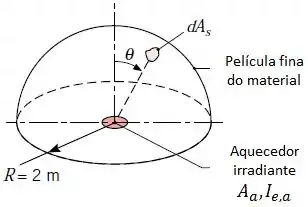
Obtenha uma expressão para a irradiação sobre a película como um função do ângulo de zênite .
Passo 1
A irradiação sobre a superfície infinitesimal está associada com a taxa de energia por radiação da seguinte forma:
Onde a taxa de energia por radiação é dada por:
Onde o ângulo sólido é dado por:
Finalmente, a irradiação será:
Resposta
Exercícios de Livros Relacionados
Quando a variação da quantidade de radiação espectral com comprimento de onda é conhecida, como é determinada a quantidade total correspondente?
Considere que a intensidade da radiação solar incidente sobre a superfície terrestre pode ser expressa como I i = 100 cos θ , onde I i tem as unidades de W / m 2 . s r . Determine o valor de pico da
Uma pequena superfície de área emite radiação como um corpo negro a T 1 = 1000K . Um detector de radiação ( A 2 ) é colocado à direção normal de visualização da superfície A 1 , a distância L, como mo
Considere uma abertura de 10m m de diâmetro onde a radiação é emitida como um corpo negro com poder emissivo de 2,87 × 10 - 5W / m ² ². O sensor de radiação é posicionado com 30 ° de inclinação fora d
Uma pequena superfície de área A = 1c m ² ² é submetida a uma radiação incidente de intensidade constante I i = 2,2 × 10 4W / m 2 . s r ao longo de todo hemisfério. Determine a taxa em que a energia d