Uma fornalha com uma abertura de de diâmetro e poder emissivo de é usada para calibrar um medidor de fluxo térmico que tem uma área sensora de .
A qual distância, medida ao longo da normal a partir da abertura, o sensor deve ser posicionado para receber uma irradiação de ?
Se o sensor for inclinado para fora da normal em , qual será a sua irradiação?
Passo 1
A qual distância, medida ao longo da normal a partir da abertura, o sensor deve ser posicionado para receber uma irradiação de ?
Vamos primeiro entender o problema: repara que o sensor está posicionado de frente pra abertura da fornalha. Então a “linha” que une essas duas superfícies passa exatamente pela normal deles, de modo que .
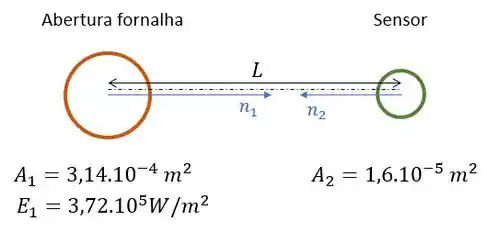
Aí em cima indicamos também a , calculada a partir do diâmetro dado, a dada e o dado.
E a gente quer saber qual deve ser a distância entre a abertura da fornalha e o sensor para que a irradiação recebida pelo sensor seja igual a
Passo 2
Então vamos colocar isso em fórmulas.
A irradiação entre a fornalha e o sensor pode ser escrita como:
Onde a taxa de calor que sai da fornalha e atinge o sensor é dada por:
Supondo que as áreas do sensor e a abertura na fornalha sejam muito menores que a distância entre elas, o ângulo sólido pode ser calculado da seguinte forma:
Além disso, considerando que a fornalha emite calor difusamente, a intensidade de radiação será dada por:
Assim, substituindo tudo isso na expressão da taxa de energia de radiação, teremos que:
Passo 3
Reorganizando os termos da equação que encontramos no passo anterior:
Onde a taxa de energia de radiação é dada por:
Dessa forma, a distância entre as placas será:
Onde:
Substituindo os valores:
![]()
Passo 4
Se o sensor for inclinado para fora da normal em , qual será a sua irradiação?
Agora a gente já sabe a distância entre as superfícies, então só precisa girar um pouquinho o sensor assim:
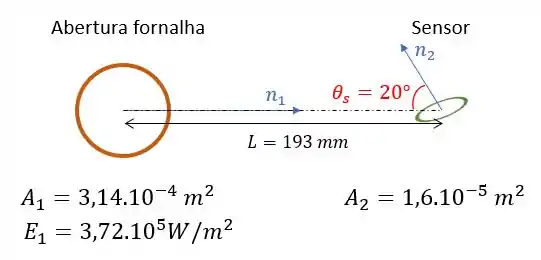
Nesse caso, a irradiação será dada por:
![]()
Resposta