Uma pequena fonte de radiação emite difusamente com uma intensidade . O detector de radiação está alinhado normal à fonte a uma distância de .
Uma tela opaca está posicionada na meta de do caminho entre e para impedir que a radiação da fonte atinja o detector. A pequena superfície é um espelho difuso perfeito que permite que a radiação emitida pela fonte seja refletida para o detector.
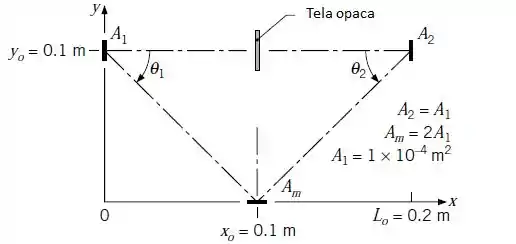
Calcule a potência radiante incidente em devido à emissão a partir da fonte , .
Supondo que a potência radiante, seja refletida perfeita e difusamente, calcule a intensidade deixando , .
Calcule a potência radiante incidente em devida à radiação refletida deixando , .
Passo 1
Calcule a potência radiante incidente em devido à emissão a partir da fonte , .
A potência radiante que sai de e atinge é dada por:
Supondo que as áreas e sejam muito menores que a distância entre elas, o ângulo sólido pode ser calculado da seguinte forma:
Onde e .
Voltando à expressão da potência radiante:
Substituindo os valores:
![]()
Passo 2
Supondo que a potência radiante, seja refletida perfeita e difusamente, calcule a intensidade deixando , .
Se a radiação for refletida difusa e perfeitamente, a intensidade de radiação que deixará será:
![]()
Passo 3
Calcule a potência radiante incidente em devida à radiação refletida deixando , .
A potência radiante pode ser escrita da seguinte forma:
Onde o ângulo sólido pode ser aproximado por:
Assim, a potência radiante será:
Substituindo os valores:
![]()
Resposta