Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Intensidade de Radiação

Ver Teoria
Exercício 31245678

Enunciado

Uma pequena superfície estacionária de área A 1 = 10 - 4 m 2 emite difusamente com uma intensidade total de I e = 100   W / ( m 2 . s r ) .

Uma segunda superfície de área equivalente A 2 = 10 - 4   m 2 está localizada a uma distância fixa de r = 0,5   m de A 1 . A linha de conexão entre as duas superfícies permanece perpendicular a A 1 , enquanto A 2 gira a uma frequência angular θ ˙ 2 = d θ 2 / d t = 2   r a d / s .

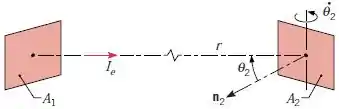
Qual é a quantidade de energia interceptada pelos dois lados de A 2 durante uma volta completa?

Passo 1

A taxa de energia emitida por A 1 e interceptada por A 2 é dada por:

q = I 1 . A 1 . cos ⁡ θ 1 . d ω 1 → 2

Como as dimensões das placas são muito menores do que a distância entre elas, podemos tratar o ângulo sólido da seguinte forma:

d ω 1 → 2 ≅ A 2 . cos ⁡ θ 2 r 2

Assim, a taxa de transferência de calor será dada por:

q = I 1 . A 1 . cos ⁡ θ 1 . A 2 . cos ⁡ θ 2 r 2

Além disso, como a linha que liga as duas placas é perpendicular à placa A 1 , θ 1 = 0 ° → cos ⁡ θ 1 = 1 . Logo:

q = I 1 . A 1 . A 2 . cos ⁡ θ 2 r 2

Passo 2

O problema nos pediu pra calcular a energia interceptada pela placa A 2 em uma volta completa.

A taxa de energia de radiação que calculamos no Passo 1 pode ser escrita como:

q = d E d t → Δ E = ∫ 0 T q . d t

Substituindo a expressão que encontramos no Passo 1:

Δ E = ∫ 0 T I 1 . A 1 . A 2 . cos ⁡ θ 2 r 2 . d t

Nessa expressão, somente θ 2 varia com o tempo, onde a velocidade angular é dada por:

θ ˙ 2 = d θ 2 d t → d t = d θ 2 θ ˙ 2

Na hora de definir os limites de integração, temos que ter muito cuidado aqui!

Em uma volta completa, o ângulo entre a linha que liga as duas placas e a linha normal à placa 2 irá variar de 0 a π / 2 quatro vezes. Sendo assim, podemos fazer os limites integração 0 ≤ θ 2 ≤ π / 2 e multiplicar a expressão inteira por 4.

Extamos fazendo isso porque, se fizermos o ângulo variando entre 0 e 2 π , a integral será igual a zero, e serio o mesmo que dizer que nenhuma energia interceptou a placa 2, o que estaria errado.

Sendo assim:

Δ E = 4 . I 1 . A 1 θ ˙ 2 . A 2 r 2 ∫ 0 π / 2 cos ⁡ θ 2 . d θ 2

Passo 3

Fazendo a integral:

Δ E = 4 . I 1 . A 1 θ ˙ 2 . A 2 r 2 ∫ 0 π / 2 cos ⁡ θ 2 . d θ 2 = 4 . I 1 . A 1 θ ˙ 2 . A 2 r 2 . sen ⁡ θ 2 0 π / 2

Δ E = 4 . I 1 . A 1 θ ˙ 2 . A 2 r 2

Substituindo os valores:

Δ E = 4 × 100 × 10 - 4 2 . 10 - 4 0,5 2

Resposta

Δ E = 8 × 10 - 6   J

Exercícios de Livros Relacionados

Quando a variação da quantidade de radiação espectral com comprimento de onda é conhecida, como é determinada a quantidade total correspondente?
Considere que a intensidade da radiação solar incidente sobre a superfície terrestre pode ser expressa como I i = 100 cos ⁡ θ , onde I i tem as unidades de W / m 2 . s r . Determine o valor de pico da
Uma pequena superfície de área emite radiação como um corpo negro a T 1 = 1000K . Um detector de radiação ( A 2 ) é colocado à direção normal de visualização da superfície A 1 , a distância L, como mo
Considere uma abertura de 10m m de diâmetro onde a radiação é emitida como um corpo negro com poder emissivo de 2,87 × 10 - 5W / m ² ². O sensor de radiação é posicionado com 30 ° de inclinação fora d
Uma pequena superfície de área A = 1c m ² ² é submetida a uma radiação incidente de intensidade constante I i = 2,2 × 10 4W / m 2 . s r ao longo de todo hemisfério. Determine a taxa em que a energia d