Considere as seguintes afirmações:

I. O produto vetorial de dois vetores unitários não é um vetor unitário.

II. Para quaisquer dois vetores e e v, u x v != v x u.

III. Para quaisquer três vetores u, v e w (u x v) = u (v x w).

Escolha uma:

a. As afirmativas I e II são verdadeiras.

b. As afirmativas II e III são verdadeiras. X c. Todas as afirmativas são falsas.

d. Todas as afirmativas são verdadeiras.

e. Apenas a afirmativa I é verdadeira.

f. Apenas a afirmativa III é verdadeira.

g. Apenas a afirmativa Il é verdadeira.

h. As afirmativas I e lll são verdadeiras.

I. Um vetor unitário , tem por definição , assim o produto vetorial entre dois vetores unitários e será:

Assim o produto vetorial entre dois vetores unitários seria o vetor com o modulo igual ao seno do ângulo entre os vetores e perpendicular a ambos (seguindo a regra da mão direita).

Verdadeiro, pois seno de um ângulo entre dois vetores não necessariamente é unitário.

II. E para quaisquer dois vetores e podemos lembrar da regra da mão direita onde dependendo da ordem em que multiplicamos os vetores o versor muda o seu sentido.

Assim temos que . (Propriedade da anticomutatividade)

E, portanto:

Logo esse item é verdadeiro.

III. Para o caso de:

Podemos utilizar a definição matricial do produto vetorial:

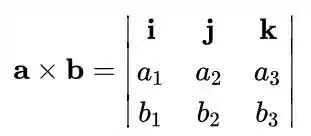
Assim realizando o produto escalar:

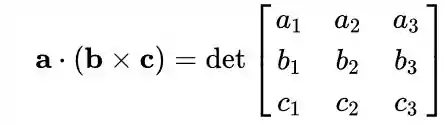
E ao lembrar da propriedade dos determinantes que ao alterar a ondem de duas linhas não alteramos o valor do determinante, podemos dizer que:

Assim provamos que:

Sendo a alternativa verdadeira.