Por meio de desenhos simples dos produtos vetoriais aproximados, demonstre que pode ser interpretado como o produto do módulo de vezes o componente de perpendicular a ou o módulo de vezes a componente de perpendicular a
Passo 1
Sabemos que a fórmula do módulo de um produto vetorial é:
O que vamos fazer é demonstrar através da área de um paralelogramo que conseguimos encontrar essa fórmula.
Passo 2
O paralelogramo formado pelos vetores tem a seguinte forma:
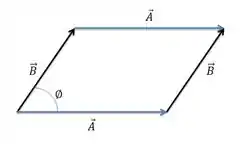
Para calcular a área desse paralelogramo vamos dividir ele em dois triângulos, pois assim podemos usar a fórmula da área que ele deu.
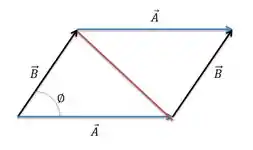
Passo 3
Como podemos perceber, divimos á area do paralelogramo em dois triângulos iguais, ou seja, se acharmos a área do triângulo conseguimos achar a área do paraleogramo.
Para calcular a área do triângulo precisamos achar a altura relativa a base.
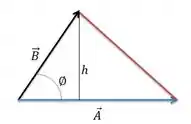
Considerando a altura relativa à base, ou seja, a componente vertical de em relação à temos que:
Passo 4
Como a fórmula da área de um triângulo é:
Substituindo os valores temos:
Escrevendo em função de :
Como já sabemos á relação da área do triângulo e do paralelogramo temos que:
Logo, como podemos ver, um produto vetorial pode ser escrito como:
onde é a componente de perpendicular a .
Resposta
Ei, a resposta está no passo a passo :)