Duas partículas estão restritas a mover-se no plano . O movimento destas partículas é descrito pelas funções posição , e , onde a posição é medida em metros e o tempo em segundos.
b) Para , faça um esquema no plano cartesiano dos vetores , e Calcule a distância entre as partículas.
Passo 1
Faaaaala pessoal, como vocês estão?
Nessa questão temos duas partículas se movimentando no plano do , o plano . Vimos, no item anterior, que o seu movimento pode ser representado pelos seguintes vetores no plano:
E, ainda, o vetor posição relativa entre as duas partículas é dada por:
A partir dessas informações, precisamos desenhar um esquema no plano cartesiano desses vetores quando . E, ainda, determinar a distância entre as partículas nesse instante, beleza?
Pra determinar a posição das partículas quando , basta substituirmos na expressão de e . Já pra calcular a distância entre as partículas nesse instante, como já temos o vetor distância relativa, basta calcularmos o seu módulo nesse instante.
Vem com a gente que vai ficar bem claro 😊
Passo 2
Bom, vamos começar esboçando os vetores posição quando .
Para a partícula , temos:
Fazendo , vem que:
Logo:
Excelente!
Já para a segunda partícula, temos:
Fazendo , vem que:
Logo:
Massa! Agora é só desenharmos no plano cartesiano. No caso do vetor , por exemplo, o nosso vetor encerra-se num ponto deslocado unidade para a direita no eixo horizontal e unidades para cima no eixo vertical.
Assim, vamos ter:
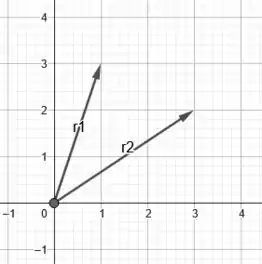
Muito bom 😊
Passo 3
Para esboçar a distância entre esses vetores, vamos calcular o módulo de quanto .
Temos:
Se , vem:
Vamos então calcular o módulo desse vetor:
Prontinho! Essa é a distância entre as duas partículas quando 😊
Valeu pessoal!