Um canal retangular com 2 m de largura e inclinação de 0,0005 possui uma profundidade de escoamento de 1,5 m. O coeficiente de rugosidade de Manning é de 0,015. Determine a descarga uniforme em regime permanente no canal.
Passo 1
Vamos começar ilustrando o escoamento e identificando as variáveis dadas no enunciado? Partiu!
O canal é retangular, então essa é uma visão de um corte nele:
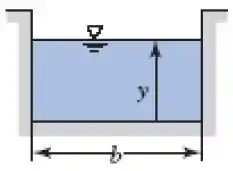
Do enunciado sabemos que
O exercício pede a descarga uniforme desse escoamento permanente. Ou seja, queremos saber a vazão! Na teoria, vimos uma fórmula que Manning ajudou a simplificar para achar a velocidade. 😉
A partir da velocidade, conseguimos encontrar a vazão volumétrica, já que: . Então vamos substituir o V
Lembrando que a área é a área da seção transversal (justamente a área do corte)
Além disso, o raio hidráulico é
Afinal, quem é o perímetro molhado ? É o somatório dos comprimentos em que o fluido toca no canal. O perímetro molhado é a parte laranja (destacada) da figura:
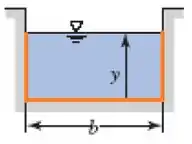
Atualizando o raio hidráulico
Show! Substituindo essa galera toda aí na expressão da vazão
Passo 2
Agora que conhecemos todas as variáveis, vamos substituir
Fazendo as contas na calculadora
Essa é a descarga uniforme em regime permanente 😉